Contents:
- Analysing a roller coaster ride
- Solving the brachistochrone problem by analogy with Fermat's principle
- Solving the brachistochrone problem directly using variational calculus
- Appendix: Using variational calculus to derive equations of motion
Analysing a Roller Coaster Ride
A roller coaster ride begins with a cable hauling a train of cars up to the top of a steep grade and releasing them. From this point on the train is powered by gravity alone and the ride can be analysed by using the fact that as the train drops in elevation its potential energy is converted into kinetic energy.
Potential Energy in a Gravitational Field
Gravitational potential energy is the energy that an object possesses by virtue of its height in a gravitational field. It is given by the formula:
where m is the mass of the object, g is the acceleration due to gravity (the gravitational constant), namely 9.81 m/s2, and h is the height of the object. If the object is raised then it gains this much potential energy; if the object is lowered then it loses this much potential energy.
In the SI (metric) system of units:
- m is expressed in kg (kilograms),
- g is expressed in m/s2 (meters per second squared),
- h is expressed in m (meters),
- the energy is expressed in J (joules).
Potential energy (in fact any type of energy) can be converted into other forms of energy. For example if an object is dropped then it speeds up (gains kinetic energy) as at falls (loses potential energy).
Kinetic Energy
Kinetic energy is the energy that an object has by virtue of its motion. It is given by the formula:
where m is the mass of the object and v is its velocity.
In the SI (metric) system of units:
- m is expressed in kg (kilograms),
- v is expressed in m/s (meters per second),
- the energy is expressed in J (joules).
Notice that if the velocity of an object is doubled, its kinetic energy is quadrupled.
Kinetic energy can be converted back into potential energy. For example on mountain roads runaway lanes are often provided for trucks that lose their brakes while going down long hills. The runaway lane takes the truck back uphill and allows the truck to coast to a stop as its kinetic energy is converted to potential energy.
Analysing the Ride

This analysis will require the use of calculus (differentiation and integration). Refer to the graph. Most roller coasters have to fit inside a limited area at the fair grounds and have twists and turns but we will assume that we can straighten out the train's path and describe it by some formula, y=y(x), where y is the vertical coordinate of the train (but notice that the y axis points downward) and x is the horizontal coordinate.
Assume that the beginning of the ride is at the origin and that the train starts there from rest (i.e. with zero kinetic energy, but of course with lots of potential energy). At any point (x, y) on the train's path the potential energy that the train has lost is mgy. This potential energy is converted to kinetic energy (assuming there are no losses to friction), so we can write the equation:
Solving for v gives us our basic formula:
|
|
(1) |
This formula tells us how the train's velocity is related to the elevation drop. We have used functional notation and written y(x) and v(x) instead of just y and v to emphasize the fact that the elevation drop and velocity are both functions of x.
Next, we must recognize that the velocity v in equation (1) is supposed to be measured along the curve. We must express the velocity in terms of its horizontal and vertical components. To do this, take a look at the small blue triangle in the graph above. Let s represent distance measured along the curve. Then:
- ds represents a small incremental distance along the curve
- dx and dy represent the horizontal and vertical components of ds
- ds, dx and dy are related by Pythagoras' theorem, which we can write as:

|
(2) |
Taking ds, dx and dy and dividing each of them by dt gives us various velocities:
- ds/dt represents the velocity, v, along the curve
- dx/dt represents the x component of the velocity
- dy/dt represents the y component of the velocity
- Note that dy/dx represents the slope along the curve, or the derivative of the curve. From now on we will write it as y'(x).
- Equation (2) becomes:
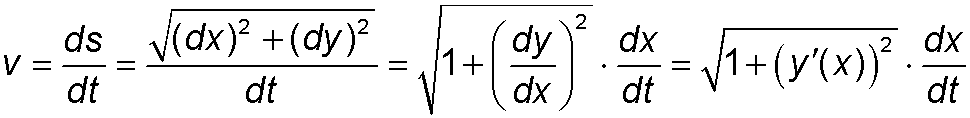
|
(3) |
Substituting this expression for v into equation (1) gives:
This can be manipulated to give:

Since the right-hand-side is a function only of x, we can integrate over x and get our final equation:
 |
(4) |
Notes on equation (4):
- The roller coaster's curve, y(x), must still be specified. It, and its derivative y'(x), are then substituted into the integral on the right-hand-side.
- Once the integration is carried out we have an answer in the form t(x) (i.e. an answer that gives the time when the train is at a specified position.) If we want x(t) (the position at a specified time) then we need to solve our answer for x. This is only possible in the simplest cases (like the following example of a ramp).
- The integration constant can be set by using the fact that x=0 at t=0.
Example: Suppose that the roller coaster's curve is given by the formula y(x)=kx. This describes a simple ramp with slope k. The derivative is y'(x)=k. Substitute these both into equation (4). This is one of the few examples where the integration is easy to do:
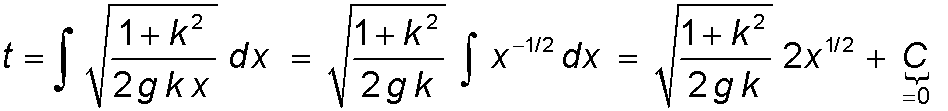
Note that the integration constant is zero. To make our answer look more familiar, let's solve it for x. This gives:
Now let's replace x (the horizontal distance) with s (the distance along the ramp) using
Then we get:
|
|
(5) |
This result was discovered experimentally by Galileo in 1638. It shows that a mass going down a ramp undergoes constant acceleration, a, and furthermore, the acceleration is the fraction of g stated in the second part of (5).
The Brachistochrone Problem

Brachistochrone is Greek for "shortest time". The brachistochrone problem is to find the curve that the roller coaster should take between points A and B to yield the shortest time for the ride. (This is another way of saying "to have the fastest average speed".)
The picture above shows three different curves. It turns out that curve 1, called a cycloid, has the shortest time. Click here to see an animation.
This problem was originally posed as a challenge to other mathematicians by Johann Bernoulli in 1696. To mathematicians this is like being challenged to a duel except the winner gets glory and nobody gets hurt. Newton and Leibniz, the two inventors of calculus, as well as Johann himself and his brother Jakob Bernoulli, all solved it using very different methods. The reason that this problem is so important is that it led to many advances in math – probably the most important being the invention of variational calculus.
As happens so often in math and science, an idea in one area can help solve a
seemingly unrelated problem in another area. In this case the idea is Fermat's Principle.
It states that light always travels along the path that takes the least time.
This will help us find the roller coaster curve that takes the least time.
Thus we must digress for a moment and look at Fermat's Principle.
Fermat's Principle

You are probably familiar with the bending (refracting) of a ray of light as it enters the water. The picture shows an example. To get from point A to point B the light ray follows path ACB and not ADB.
In 1662 Fermat proposed an explanation: the speed of light is lower in water than air, and the path taken by a light ray between two given points is the one that can be traveled in the least time. This is now called Fermat's Principle.
Here is an analogy: suppose that the same picture describes a lifeguard at point A on the beach and a drowning swimmer at point B
in the water. Running is much faster than swimming so it is quicker for the lifeguard to follow path
ACB to get to the swimmer than path ADB.
Fermat's Principle was initially controversial because it seemed to imply that nature was able to test alternative paths. We now know that it is actually a fundamental property of waves.
Click here to see a simulation of the connection between waves and refraction.
Snell's Law
Snell's Law follows directly from Fermat's Principle. It gives the amount of refraction. It states that when a light ray goes from a medium where its velocity is v1 to a medium where its velocity is v2, it is refracted and follows a path governed by the equation
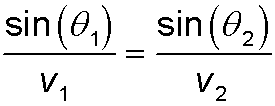
|
(6) |

The angles θ1 and θ2 are defined in the picture. The light ray is shown in red. θ1 is called the angle of incidence and θ2 is called the angle of refraction. (It is useful to think of the law as saying that the ratio sin(θ)/v remains constant. Essentially big v, big θ; small v, small θ.)
We will now derive Snell's Law from Fermat's Principle. To make the trigonometry easy, let the ray start at (−1, 1)
and end at (1, −1). Let the ray cross the x axis at some unknown location, x.
Let s1 be the length of the ray in medium 1
and s2 be the length of the ray in medium 2.
Then the time that the ray spends in medium 1 is s1/v1
and the time it spends in medium 2 is s2/v2.
The total time t is given by:
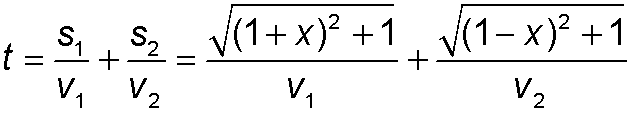
|
(7) |

The last expression follows from Pythagoras' theorem applied to the two gray triangles.
The picture to the right shows a graph of equation (7). Notice that the time t does indeed have a minimum at some value of x. Fermat's Principle states that the path that the light ray actually takes will be the one with this value of x.
To find the minimum we take the derivative of equation (7):

and set it to zero:

Then we recognize that the blue expression is sin(θ1) and the red expression is sin(θ2), so we have Snell's Law.
Bernoulli's Solution of the Brachistochrone Problem
Johann Bernoulli solved the Brachistochrone Problem by making an analogy between the curve followed by the roller coaster and the path followed by a light ray. The shortest time curve for the roller coaster (the brachistochrone) is analogous to the path followed by a light ray obeying Fermat's Principle.
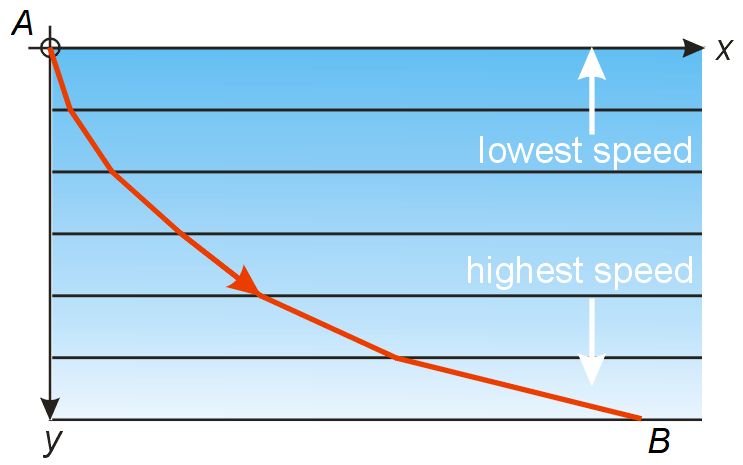
The only difference is that the light ray passes through just two regions (air with a high speed and water with a low speed), whereas the roller coaster passes through a continuum of horizontal layers, and the speed of the roller coaster is different in each layer. See the picture to the right. Also, because of the energy formula ½mv2=mgy, the slowest layers are at the top and the fastest layers are at the bottom.
Continuing the lifeguard-swimmer analogy, suppose swimming is slow near the shore (top of the picture) perhaps because of big waves, and is faster farther out (bottom of the picture). Then to get from A to B it is better to keep the low-speed part of the swim as short as possible. This means the path should bend as shown.
Applying Snell's Law
Snell's Law sin(θ1)/v1=sin(θ2)/v2 can be interpreted as saying that the ratio sin(θ)/v remains constant along the brachistochrone.

Look at the picture to the right. At the beginning of the ride, point A, the velocity v is zero and Snell's Law says that the angle θ must also be zero. In other words the curve starts vertically. As the ride progresses, v gets bigger and Snell's Law says that θ gets bigger.
At some point B the sine function reaches its maximum value, 1, the angle is 90° meaning that the ride levels out, the vertical drop is at a maximum, and the velocity is at a maximum. Call the vertical drop at this point ymax and the velocity at this point vmax.

The table shows what happens to various quantities at point B. The last 2 rows follow from the picture to the right.
| quantity | anywhere along the curve |
at point B |
|---|---|---|
| angle | θ | 90° |
| velocity | ||
| vertical drop | y | ymax |
| incremental drop | dy | 0 |
| incremental distance along the curve |
ds=dx |
Let's derive the equation for the brachistochrone. Start with Snell's Law:

Substitute in quantities from the table:

Solve for dx:
 |
(8) |
Equation (8) is a so-called separable differential equation. Its solution is the equation for the brachistochrone. The solution is:

|
(9) |
This type of curve is called a cycloid. It is expressed in parametric form, which means that if we put in a value for the parameter θ then we get out a value for x and a value for y. Putting in a sequence of values for θ gives us a sequence of points along the curve.
We won't try to derive the brachistochrone solution (9) from the separable differential equation (8) because it is quite technical, but we can easily verify that it is correct by differentiating both of the equations in (9) and getting back the differential equation in (8).

Cycloid
The cycloid is the curve traced out by a dot on the rim of a wheel as it rolls along a straight line without slipping. Here is a picture:

Click here to see an animation. The wheel, with radius a, is shown in gray and the cycloid is shown in red. θ measures the angle through which the wheel has rotated in radians. The parametric equations for the cycloid are also displayed in the picture.
The parametric equations might make more sense if we write them as the sum of two vectors. The first vector is from the center of the wheel to its edge. The second vector is from the origin to the center of the wheel.
Below is a picture of the first vector (top) and the second vector (bottom) for various values of θ:

Note that because the circle rolls without slipping, each cycle of the cycloid has a width 2πa and height 2a. In other words, a very definite ratio of width to height, namely π to 1.
To turn the graph of the cycloid into the graph of the brachistochrone we need to do several things:
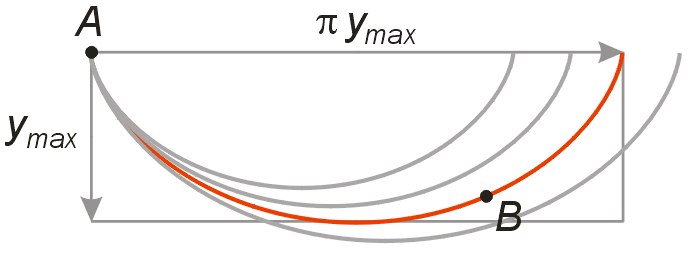
- Turn the cycloid upside-down (since the y axis for the cycloid points upward whereas the y axis for the roller coaster points downward).
- Put the cusp (sharp point) of the cycloid at the start point, A.
- Scale (stretch) the cycloid so that it passes through the endpoint, B.
- Replace the radius a in the parametric equations for the cycloid with ymax/2 to get the parametric equations for the brachistochrone. Notice that in general, endpoint B is not at the height ymax. In fact, in the picture below, end points B1, B2 and B3 would all have the same value of ymax.
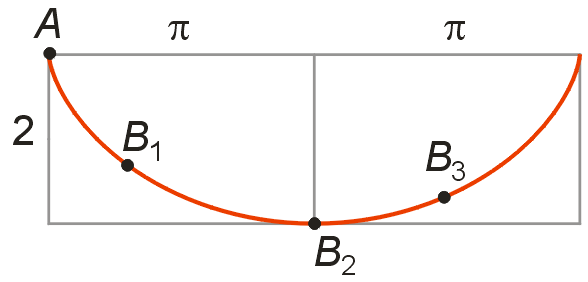
Two more points:
- The turning upward of the brachistochrone at point B2 is the analog of total internal reflection in optics.
- Our differential equation, (8), doesn't contain time so its solution, the equation for the brachistochrone, doesn't contain time either. However it can be shown that the parameter θ is proportional to time:
Solving the Brachistochrone Problem Using Variational Calculus
Fermat's Principle (that light follows the path of shortest time) has intrigued mathematicians and physicists ever since it was proposed. It turns out that there are many similar principles in nature. Variational calculus allows us to derive equations from these principles.
To put variational calculus into context, let's first understand why ordinary calculus (calculus of one variable) was sufficient for us to derive Snell's Law, above. (Click here to see that again.) The key is the assumption that the light ray's path is straight except at one point on the interface, where it is bent. This assumption allows us to write down a formula that gives the travel time, t, as a function of a single variable, namely the point x on the interface. Then we can use the fact that in order for the function t(x) to have a minimum, it is necessary that the derivative dt/dx is zero. Applying this condition gives Snell's Law. This box summarizes the situation:

Single-variable calculus. (left) The gray box represents a function (a number x goes in and a number t comes out). (middle) Graph of the function. For a certain value, denoted x*, the function is a minimum. (right) At the minimum the equation dt/dx = 0 holds. Solving this equation gives x*.
Now let's take another look at the roller coaster formula, equation (4),

which we derived previously. (Click here to see that again.) For a roller coaster following any curve y(x), this formula gives the time t when the roller coaster is at the point x.
Suppose that we are only interested in the total ride time tAB between some starting point A and some ending point B. We can get that by turning the roller coaster formula into a definite integral:
 |
(10) |
This type of formula is called a

It works like this: Imagine taking many different curves y(x) that start at point A and end at point B, and plugging them into the functional and finding the time tAB for each one. We could then pick the curve with the smallest tAB and this would be the brachistochrone.
There is a type of calculus that can do this – it is called
variational calculus.
The key result of variational calculus is that if a functional
|
|
(11) |
has a local minimum, then the integrand of the functional, L(y, y', x), must obey the Euler–Lagrange equation,
|
|
(12) |
In general the Euler-Lagrange equation gives a second-order ordinary differential equation which can be solved to obtain the function y(x) that minimizes the functional.
Some notes on the notation:
- The integrand of the functional, L(y, y', x), is called the Lagrangian.
- The Lagrangian can contain the function y, its derivative y' and the x coordinate itself. For example the Lagrangian for the brachistochrone problem contains y and y'. The variable x is absent:

- In the Euler-Lagrange equation the notation ∂L/∂y means that we should treat y as a variable and every other symbol as a constant and take the derivative of L with respect to y. Similarly, ∂L/∂y' means that we should treat y' as a variable and every other symbol as a constant and take the derivative of L with respect to y'.
The box below summarizes variational calculus. Check out how it compares to single-variable calculus, which was summarized in the previous box.

Variational calculus. (left) The gray box represents a functional (a function y(x) goes in and a number tAB comes out). (middle) Representation of the functional. (Artistic license – it isn't actually possible to plot functions on an axis.) For a certain function, denoted y*(x), the functional is a minimum. (right) The integrand of the functional is called the Lagrangian, denoted L. At the minimum the Euler-Lagrange equation holds. Solving it gives y*(x).
Example: Solve the Brachostochrone problem using variational calculus.
Solution: We won't give the details because they are too technical but you can find them here. Here are the pieces:
The functional to be minimized is:

The Lagrangian (the integrand) is:

The Euler-Lagrange equation (after an integration and much simplification) is:
After rearranging, this is the same separable differential equation, (8), that we found above, and whose solution is the cycloid.

Example: Prove that the shortest curve connecting points A and B is the straight line. (We choose this problem because it is simple enough that we can actually carry out all the steps!)
Solution: When we analysed the roller coaster above we defined ds as a small incremental distance along a curve.
The length s of the entire curve is found by integrating this.
Thus the length s is a functional. Its integrand, the Lagrangian, is:
Notice that x and y are both absent. For the shortest curve it satisfies the Euler-Lagrange equation. Here it is:
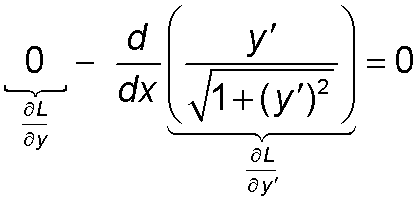
To solve this equation, first integrate with respect to x. (C is the integration constant.)
Next solve for y'. It equals another constant, which we will call m. Finally, integrate one more time with respect to x, and we have the equation of a straight line.
This proves that the curve of shortest length is the straight line.
Appendix: The Stationary Action Principle and Laws of Motion
The Stationary Action Principle (also known as the least action principle) is similar to Fermat's least time principle. This principle can be used to derive Newton's laws of motion. When generalized, it can even be used to derive the equations describing electromagnetism, quantum mechanics, quantum field theory and general relativity.
The Stationary Action Principle states that the trajectory taken by a particle or system between an initial point x1=x(t1) and a final point x2=x(t2) is the one for which the action is stationary. The action is defined as the functional:
where the integrand (the Lagrangian) is:
The first term, KE = ½ m ẋ 2, is the kinetic energy of the system. The second term, PE, is the potential energy and it can take various forms, depending on the system. Stationary means that δS/δx = 0 (i.e. S could be a local maximum, local minimum or saddle point).
Notation Used in This Section
In the previous section we described curves in space: cycloids, straight lines, etc. In this section we want to describe the trajectory of a particle or system as a function of time. Therefore we are going to change the notation from that of the previous section.
- Let x denote the position of a particle and t denote the time. Finding x(t), the position of the particle as a function of time, (i.e. the trajectory), is our goal.
- The derivative dx/dt will be denoted as ẋ and spoken as “x dot” and will repesent the velocity of the particle. Using a dot is called Newton's dot notation.
Changing x to t and y to x will change the appearance and meaning of various quantities that were defined in the previous section, as shown in this table:
| quantity | previous section | this section |
|---|---|---|
| the function |
y(x), describes a curve |
x(t), describes a trajectory |
typical graph |
 |
 |
| the function's derivative |
y'=dy/dx = slope | ẋ=dx/dt = velocity |
| Lagrangian | L(y, y', x) | L(x, ẋ, t) |
| functional | ||
| Euler-Lagrange equation |
 |
The box below summarizes the Stationary Action principle. Compare this box to the one for single variable calculus and the one for the variational calculus of curves.

Stationary Action Principle. (left) the gray box represents the action functional (a trajectory function x(t) goes in and an action value S comes out). (middle) Representation of the action functional. (Artistic license – it isn't actually possible to plot functions on an axis.) For a certain trajectory, denoted x*(t), the action functional is stationary. (right) The integrand of the functional is called the Lagrangian, denoted L, and it equals the kinetic energy minus the potential energy of the system. At the stationary point the Euler-Lagrange equation holds. It gives an equation of motion. Solving it gives x*(t).

Example: The picture shows a mass on a spring. The mass can only move in the x direction. When the mass's position, x, is positive, the spring is stretched. When it is negative, the spring is compressed. Derive the equation of motion for this system.
Solution: The kinetic energy of the mass is KE = ½ m ẋ 2. The potential energy stored in the spring when it is stretched or compressed by an amount x is PE = ½ k x 2. Therefore the Lagrangian is:
The Euler-Lagrange equation,
becomes
This differential equation is the equation of motion for the mass-spring system. We won't derive its solution, but it is easy to check by back-substitution that it is:
A and φ are arbitrary constants. This is an oscillation like the one shown in the graph in the table above.
If you would like to leave a comment or ask a question please send me an email!
