MathOnWeb.com

Click here to download a zip file containing all the Book 1 resources, or you can click on the links below to download them individually. (On some browsers you may need to right-click and choose 'save link as ...' ).

• Basic Maple commands. This Maple workbook introduces you to the basic Maple commands for solving equations, plotting functions, working with vectors and matrices, and working with complex numbers in polar and rectangular coordinates. It relates to Chapter 1, page 33 of the book.
  
  
  
• The bisection method. This is an Excel spreadsheet that shows you how to find the roots of an equation using the bisection method. Programmers: See how to do this with a Visual Basic function. It relates to the computer code in Chapter 1, page 30 of the book.
  
  



• The Gauss-Jordan elimination method. This Excel spreadsheet does Gauss-Jordan elimination. Programmers: See how this is done with a VB subroutine (macro). Relates to the computer code in Chapter 2, page 48.
  
  



• Matrix arithmetic in Excel. This spreadsheet shows how matrix arithmetic is implemented in Excel. Relates to Chapter 3, page 96.
  
  



• Calculating loans and mortgages. This Excel spreadsheet shows how a debt grows when a loan has different types of compounding applied, and how a mortgage is paid off. Relates to Example 4.20.
  
  



• Calculating AC power. This Excel spreadsheet shows the instantaneous and average electric power that results when an AC current and voltage are out of phase. Relates to Example 5.14.
  
  



• e^x = limit (1+1/n)ⁿ. This Excel spreadsheet shows how e^x can be computed for any x, real or complex, as the limit of repeated multiplication. It also explains how complex numbers are implemented in Excel. Relates to Problem Set 7.3, #6.
  
  



• RLC circuits. This Excel spreadsheet shows how in an AC series circuit the values of R, L, C and ω affect the Z diagram and the phase shift between the voltage and current. Programmers: See how to write code to implement slider and button controls to set the values of R, L, C and ω. Relates to Chapter 8, page 257, and resonance.
  
  



• The Gauss-Jordan elimination method (with complex numbers). This Excel spreadsheet contains a macro that does Gauss-Jordan elimination with complex numbers. This can be used, for example, to solve AC network problems. Relates to the computer code in Chapter 8, page 276.
  
  

Click here to download a zip file containing all the Book 2 resources, or you can click on the links below to download them individually. (On some browsers you may need to right-click and choose 'save link as ...' ).

• Integration and differentiation in Maple. This Maple worksheet introduces the basic Maple commands for differentiating and integrating.
  
  
  
• The Newton-Raphson method. This Excel spreadsheet shows how to use the Newton-Raphson method to calculate square roots. Relates to Section 3.6 of the book.
  
  


• The rectangular rule, trapezoidal rule, and Simpson’s rule. This Excel spreadsheet compares numerical integration using these three methods. Programmers: See how these rules are implemented with Visual Basic functions. Relates to the computer code given in Section 6.5 of the book.
  
  


• Taylor series. This Excel spreadsheet shows how the Maclaurin series for e^x is accurate only for small x. It also shows how the Maclaurin series for ln(x) can be modified to make it accurate to 6 sig. figs for any x. Relates to Example 9.19 of the book.
  
  


• Filtering by an RLC circuit. This Excel spreadsheet uses complex arithmetic to construct the gain and phase shift graphs that describe filtering by an RLC circuit. Relates to Section 10.6 of the text.
  
  



• Fourier series of a sawtooth waveform. This Maple worksheet shows how to use Maple to calculate Fourier coefficients analytically. It shows how to correctly apply symmetry arguments to find the coefficients for the sawtooth waveform. Relates to Chapter 10, page 245.
  
  



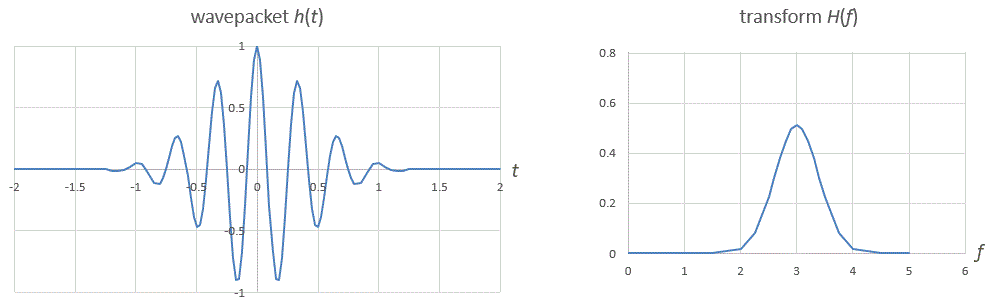
• Fourier transform of a wavepacket. This Excel spreadsheet calculates the Fourier transform of a wavepacket by doing a whole sequence of numerical integrations, one for each frequency. Relates to Example 10.14.
  
  



• FFT of a wavepacket. This Excel spreadsheet contains a Fast Fourier Transform (FFT) routine. It is used to calculate the Fourier transform of the same wavepacket as the previous spreadsheet. Relates to Example 10.15.
  
  
  
• Sunspots peak every 11 years. This spreadsheet is similar to the previous one but looks at the historical data on sunspot activity on the sun's surface and does an FFT to look for cycles. Relates to Problem Set 10.3, #6.
  
  

Click here to download a zip file containing all the Book 3 resources, or you can click on the links below to download them individually. (On some browsers you may need to right-click and choose 'save link as ...' ).

• Differential Equations in Maple. This Maple worksheet shows how to solve differential equations and initial value problems analytically. It also shows how to make direction fields like the one shown here:
  
  



• Euler’s method and the Runge-Kutta method. This Excel spreadsheet shows how to solve differential equations numerically. The first sheet uses Euler's method. The rest use the Runge-Kutta method. There are various approaches: a single DE, multiple DEs, using just the spreadsheet and utilizing Visual Basic code. Relates to Section 2.2 of the book.
  
  



• Laplace Transforms. This Maple worksheet shows how to do Laplace transforms and inverse Laplace transforms. Relates to Chapter 3.
  
  



• Discrete Functions. Shows how to use Excel to generate discrete functions using recursion relations and how to plot them. Relates to Chapter 4.
  
  



• z-Poles. This Excel spreadsheet shows how poles inside/outside the unit circle in the z domain correspond to stable/unstable discrete functions in the time domain. Refers to Figs. 5.3 to 5.8 of the text.
  
  

Click here to download a zip file containing all the Book 4 resources, or you can click on the links below to download them individually. (On some browsers you may need to right-click and choose 'save link as ...' ).

• Vectors, Curves and Motion. This Excel spreadsheet shows how some of the Chapter 1 problems can be solved numerically. For example: how to calculate tangent, normal, binormal, velocity, and acceleration vectors; and how to calculate arc length.
  
  


• Partial Derivatives. This Maple workbook shows how some of the Chapter 2 problems on partial derivatives can be solved analytically using Maple.
  
  



• Gradient Descent. This Excel spreadsheet shows how going down the gradient takes you to a local minimum. Relates to Example 2.4.
  
  



• 2D Integral Examples. This Maple workbook shows how to do double integrals as iterated integrals. Relates to Section 3.3.
  
  


• Two Charges. This Maple workbook shows how to plot the electric field and the voltage field around an electric dipole. Relates to Example 4.8.
  
  


• Green’s Theorem. This Excel spreadsheet models Green’s Theorem. It uses an irregularly shaped region and any vector field. Relates to Chapter 6 of the text.
  
  


• Surface Integrals. This Maple workbook calculates the surface integrals in Examples 7.2, 7.6 and 7.7 using the method of projecting the surface onto a coordinate plane, as described in the text.
  


• Surface Integrals Using Parametrization. This PDF document shows how to calculate surface integrals by parameterizing the surface rather than by projecting the surface onto a coordinate plane. This approach is used by Kreyszig in his book Advanced Engineering Mathematics.
  
  


• Gauss's Theorem on a Hemisphere. This Maple workbook solves Problem Set 8.1, #3 with a hemisphere of any radius and any vector field.
  
  



• Gauss's Theorem Using Parameters. This Maple workbook also solves Problem Set 8.1, #3 but parameterizes the surface as described in Kreyzig's book.
  
  



• Stokes's Theorem on a Plane Triangle. This Maple workbook solves Problem Set 8.2, #1 with any plane triangle surface and any vector field.
  
  


• Stokes's Theorem on a Plane Disk. This Maple workbook solves Problem Set 8.2, #3 with any plane disk surface and any vector field.
  
  


• Heat Equation. The heat equation is a partial differential equation that describes heat flow. This Excel spreadsheet contains computer code that can solve this equation under various boundary conditions. Relates to Section 9.6 of the chapter on partial differential equations.