The Inside / Outside Problem
A calculation that must be performed billions of times in every movie that uses CGI (computer generated imagery) is finding the parts of one object that are hidden by another object. This calculation in turn is based on another calculation that checks whether or not a test point lies inside or outside the boundary of an object.

Somehow a human can easily tell that points C and A are inside the polygon and point B is outside. But how can we program a computer to do it? This is called the inside / outside problem and in this blog page we will give an algorithm and an Excel Visual Basic program to solve it. You can save yourself some typing and download the spreadsheet here.
Points are stored in a computer as ordered pairs of (x, y) coordinates:
| A=(22, 15) B=(40,17) C=(8, 16) | (1) |
A polygon is stored as a pline – a list of points. These points are the vertices of the polygon. By letting the last vertex equal the first vertex we are indicating that the pline ends where it starts and that it represents a closed polygon (rather than just a line). Each vertex is connected to the next vertex by an edge. Here are the five vertices and the five edges for the polygon shown above.
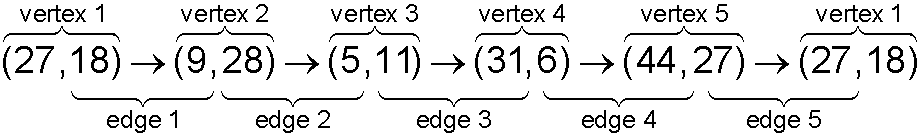
| (2) |
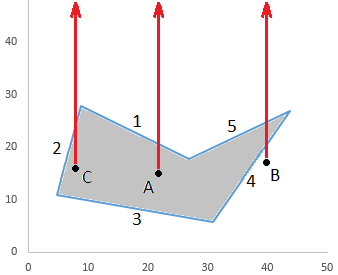
Our algorithm and program will have only numbers like those given in (1) and (2) to work with. The picture to the right shows the test points, A, B, C and the polygon with edges 1, 2, 3, 4, 5.
The picture also shows aThe basic idea of our algorithm is to count the number of times that a ray crosses the boundary of the object. If it crosses an odd number of times then the test point is inside the object. If it crosses an even number of times then the test point is outside.
In the picture we see that the rays from A and C cross the boundary once so A and C are inside the polygon. The ray from B crosses twice so B is outside.

The picture to the right shows a more complicated object. This time the ray from C crosses the boundary 3 times and the ray from B crosses twice, so C is inside and B is outside the object. (If point B was behind the object it would not be hidden. It would show through the hole.)
Algorithm to determine whether a test point is inside or outside a polygon

Here is a flowchart of the algorithm. It starts with two pretests. The first pretest checks if the test point is exactly on the boundary of the polygon. This is easy to do – the details are given later. This pretest is useful because it makes the tests that follow simpler.
The second pretest constructs the
Here are 800 random test points in and around the polygon:
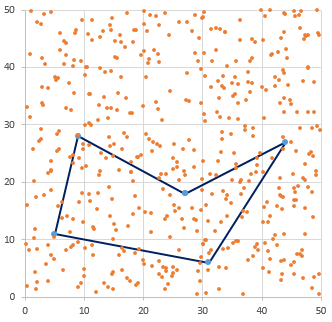
Any point outside the box is also outside the polygon. This pretest is important because it easily and quickly determines that more than 600 of the points are outside the polygon. This leaves only the points inside the box still to be checked:


Each of these points is now subjected to the tests that were described in the introduction to this blog page, namely to count the number of times that a vertical ray from the point crosses the boundary of the polygon. As shown in the flowchart, we need two variables: Edge, an index for the edge presently being tested, and Count, the number of crossings found so far.
For example, in the picture to the right Edge will run from 1 to 5. Count will start at 0, become 1 at the first edge, and remain unchanged after that.

We also need to construct the minimum bounding box for each edge.
For example, in the picture to the right, the boxes for edges 1 to 4 are shown shaded. (The box for edge 5 is shown dashed to distinguish it from the box for edge 4, which it overlaps.)
Notice that box 1 is above the test point and straddling it, box 2 is to the left, box 3 is below, and boxes 4 and 5 are to the right of the test point. Note also that if the test point was a little higher it would be inside box 1. These are some of the cases that the tests will have to deal with.

The part of the flowchart that deals with one test point and one edge has been redrawn to the right.
The first test (the first diamond in the flowchart) asks if the edge's box is (1) to the left, (2) to the right, or (3) below the test point. In any of these cases the ray cannot cross the edge so the variable Count doesn't change:

The second test (second diamond) asks if (4) the box is above and straddling the test point. In this case the ray must cross the edge so Count increases by 1.
The third test (third diamond) asks if (5) the point is inside the box. In this case the ray may or may not cross the edge as shown below. We deal with this case in a moment.

But first, are there any other possibilities? The answer is yes. The one other possibility is that the test point is (6) vertically aligned with one or more vertices, like this:

The easist way to deal with this case is to simply nudge the point to the right by some tiny amount and redo the tests.

Case (5). The test point is inside the edge's bounding box.
Assume that the test point is A = (xA, yA) and that the edge runs from (x1, y1) to (x2, y2).
The test point could be above, on, or below the edge. To decide which it is, we use the parametric form for the edge's line, namely

| (3) |
Notice that as t varies from 0 to 1, we move along the edge from the first vertex to the second. Also notice that as long as the edge is not vertical we can solve the first equation for t,
|
| (4) |
and substitute it into the second equation to get the point-slope form of the straight line.
|
| (5) |
Finally, notice that by substituting x = xA into equation (5) we can calculate yC , the y coordinate of the point on the edge where a vertical line through A would cross (the blue dot inside the bounding box).
|
| (6) |
There are 3 possibilities:
- If yC > yA , like in the picture above, then the ray does cross this edge so we increment Count by 1.
- If yC < yA then there is no crossing so we leave Count unchanged.
- If yC = yA then the test point is on the edge, i.e. on the polygon's boundary. (Note that we actually have to test if |yC − yA| < some tolerance.)
The Spreadsheet and Code
Here is the spreadsheet. The circled numbers refer to the notes below.

Notes on the spreadsheet:
- The x and y coordinates of the polygon are entered in columns A and B. We can only enter one polygon. The last vertex must equal the first vertex to close the polygon. The polygon is displayed in the chart.
- Clicking the Setup button causes the VB code to generate random test points.
- The VB code puts the x and y coordinates of the test points in columns E and F.
- Excel plots the polygon in columns A and B as lines and the test points in columns E and F as dots.
- Clicking the Run button causes VB code to apply the algorithm to all the test points. The VB code deletes any test points that are outside the polygon and Excel updates the plot to show the results.
Below is the Visual Basic code. To use it, copy both parts into an Excel module. It assumes that the spreadsheet is organized as shown above.
Option Explicit '1
Private Vertices As Integer, _
PolyX() As Single, PolyY() As Single 'Polygon vertices x & y coords. '2
Private PolyL As Single, PolyR As Single 'Bounding box (BBox) for poly. '3
Private PolyB As Single, PolyT As Single '4
Private EdgeL() As Single, EdgeR() As Single 'BBox for each edge of poly. '5
Private EdgeB() As Single, EdgeT() As Single '6
Private Const PointNum = 900, BdryWidth = 50 / 100000 '7
'----------------------------------------------------------------------------------------
Public Sub Setup() '8
'Set up the problem: read in the poly and generate random test points.
Dim I As Integer '9
For I = 3 To 1000 'Find end of the polygon '10
If Cells(I, 1) = "" Then Exit For '11
Next I '12
Vertices = I - 4 'Reserve space for the poly. '13
ReDim PolyX(1 To Vertices + 1) '+ 1 because poly is closed. '14
ReDim PolyY(1 To Vertices + 1) '15
For I = 1 To Vertices + 1 'Read in the poly. '16
PolyX(I) = Cells(I + 2, 1) '17
PolyY(I) = Cells(I + 2, 2) '18
Next I '19
Call BBoxPoly 'Set up BBox for poly. '20
'Optionally draw bounding box
' Cells(I + 11, 11) = PolyL: Cells(I + 11, 12) = PolyB
' Cells(I + 12, 11) = PolyR: Cells(I + 12, 12) = PolyB
' Cells(I + 13, 11) = PolyR: Cells(I + 13, 12) = PolyT
' Cells(I + 14, 11) = PolyL: Cells(I + 14, 12) = PolyT
' Cells(I + 15, 11) = PolyL: Cells(I + 15, 12) = PolyB
Call BBoxEdges 'Set up BBox for each edge too. '21
Range("D2:F1000").ClearContents '22
Call Rnd(-1) '23
For I = 1 To PointNum 'Put PointNum random '24
Cells(I + 1, 4) = I 'test points in columns D,E,F. '25
Cells(I + 1, 5) = Rnd * 50 '26
Cells(I + 1, 6) = Rnd * 50 '27
Next I '28
End Sub '29
'----------------------------------------------------------------------------------------
Public Sub Run() '30
'Solve the In/Out problem for all the test points.
Dim I As Integer, Result As Integer '31
Dim PtX As Single, PtY As Single '32
Dim InCount As Integer, OutCount As Integer, BdryCount As Integer '33
For I = 1 To PointNum 'Run through the test points. '34
PtX = Cells(I + 1, 5) '35
PtY = Cells(I + 1, 6) '36
Call PreTests(PtX, PtY, Result) '37
If Result = 4 Then 'Pretests are inconclusive. '38
Call Tests(PtX, PtY, Result) 'Do more tests. '39
End If '40
If Result = 1 Then 'Point is inside. '41
InCount = InCount + 1 'Count it. '42
ElseIf Result = 2 Then 'Point is outside. '43
Cells(I + 1, 5) = "" 'Delete it. '44
Cells(I + 1, 6) = "" '45
OutCount = OutCount + 1 '46
ElseIf Result = 3 Then 'Point is on boundary. '47
BdryCount = BdryCount + 1 'Count it. '48
End If '49
Next I '50
DoEvents 'Let spreadsheet update. '51
MsgBox InCount & " of " & PointNum & " points are inside the polygon." '52
End Sub '53
'----------------------------------------------------------------------------------------
Private Sub Tests(PtX As Single, PtY As Single, Result As Integer) '54
'Result: 1 = inside, 2 = outside, 3 = on bdry
Dim I As Integer, Count As Integer, T As Single, YC As Single '55
Dim Shift As Integer '56
1: '57
For I = 1 To Vertices 'Loop over the edges. '58
If PtX > EdgeR(I) Or PtX < EdgeL(I) Or PtY > EdgeT(I) Then '(1,2,3) '59
'point is to right, to left, or above edge Bbox, so Count unchanged
ElseIf PtY < EdgeB(I) And PtX > EdgeL(I) And PtX < EdgeR(I) Then '(4) '60
'edge Bbox is above, and straddling
Count = Count + 1 '61
ElseIf PtX > EdgeL(I) And PtX < EdgeR(I) _
And PtY > EdgeB(I) And PtY < EdgeT(I) Then 'case (5) '62
T = (PtX - PolyX(I)) / (PolyX(I + 1) - PolyX(I)) '63
YC = PolyY(I) + T * (PolyY(I + 1) - PolyY(I)) '64
If YC > PtY Then Count = Count + 1 '65
Else 'coincidence case (6) '66
PtX = PtX + BdryWidth 'Temporarily nudge the point right. '67
Shift = Shift + 1 'Keep track of how many shifts. '68
Count = 0 'Restart the count of crossings. '69
GoTo 1 '70
End If '71
Next I 'Next edge. '72
PtX = PtX - BdryWidth * Shift 'Move the point back. '73
If Count Mod 2 = 1 Then 'Count is Odd, point is inside. '74
Result = 1 '75
Else '76
Result = 2 'Count is Even, point is outside. '77
End If '78
End Sub '79
Private Sub PreTests(PtX As Single, PtY As Single, Result As Integer) '80
'Result 2: = outside, 3 = on bdry, 4 = inconclusive
If PtX > PolyR Or PtX < PolyL Or PtY < PolyB Or PtY > PolyT Then '81
Result = 2 'point is outside polygon's Bbox '82
ElseIf OnTheBorder(PtX, PtY) Then '83
Result = 3 'point is on poly's boundary '84
Else '85
Result = 4 'inconclusive '86
End If '87
End Sub '88
'----------------------------------------------------------------------------------------
Public Function OnTheBorder(PtX As Single, PtY As Single) As Boolean '89
'Return True if point (PtX, PtY) is on poly's border
Dim I As Integer, T As Single, XC As Single, YC As Single '90
For I = 1 To Vertices 'Is the point a vertex? '91
If PolyX(I) = PtX And PolyY(I) = PtY Then 'Point is on vertex. '92
OnTheBorder = True: Exit Function '93
End If '94
Next I '95
For I = 1 To Vertices 'Run through the edges. '96
If EdgeR(I) - EdgeL(I) > EdgeT(I) - EdgeB(I) Then 'Wide edge. '97
T = (PtX - PolyX(I)) / (PolyX(I + 1) - PolyX(I)) '98
If T > 0 And T < 1 Then '99
YC = PolyY(I) + T * (PolyY(I + 1) - PolyY(I)) '100
If Abs(YC - PtY) < BdryWidth Then 'Point is on wide edge. '101
OnTheBorder = True: Exit Function '102
End If '103
End If '104
Else 'Tall edge. '105
T = (PtY - PolyY(I)) / (PolyY(I + 1) - PolyY(I)) '106
If T > 0 And T < 1 Then '107
XC = PolyX(I) + T * (PolyX(I + 1) - PolyX(I)) '108
If Abs(XC - PtX) < BdryWidth Then 'Point is on tall edge. '109
OnTheBorder = True: Exit Function '110
End If '111
End If '112
End If '113
Next I '114
End Function '115
'----------------------------------------------------------------------------------------
Public Function Min(A As Single, B As Single) As Integer '116
If A < B Then Min = A Else Min = B '117
End Function '118
'----------------------------------------------------------------------------------------
Public Function Max(A As Single, B As Single) As Integer '119
If A > B Then Max = A Else Max = B '120
End Function '121
'----------------------------------------------------------------------------------------
Public Sub BBoxPoly() '122
'Create bounding box for the whole polygon.
Dim I As Integer '123
PolyL = PolyX(1): PolyR = PolyL: PolyB = PolyY(1): PolyT = PolyB '124
For I = 2 To Vertices '125
PolyL = Min(PolyL, PolyX(I)) '126
PolyR = Max(PolyR, PolyX(I)) '127
PolyB = Min(PolyB, PolyY(I)) '128
PolyT = Max(PolyT, PolyY(I)) '129
Next I '130
End Sub '131
'----------------------------------------------------------------------------------------
Public Sub BBoxEdges() '132
'Create bounding box for each of the polygon's edges.
Dim I As Integer '133
ReDim EdgeL(1 To Vertices) '134
ReDim EdgeR(1 To Vertices) '135
ReDim EdgeB(1 To Vertices) '136
ReDim EdgeT(1 To Vertices) '137
For I = 1 To Vertices '138
EdgeL(I) = Min(PolyX(I), PolyX(I + 1)) '139
EdgeR(I) = Max(PolyX(I), PolyX(I + 1)) '140
EdgeB(I) = Min(PolyY(I), PolyY(I + 1)) '141
EdgeT(I) = Max(PolyY(I), PolyY(I + 1)) '142
Next I '143
End Sub '144
Notes on the code:
- Lines 1 to 7 declare various global variables. Vertices is the number of vertices of the polygon (which of course equals the number of edges). PolyX(i) and PolyY(i) are the x and y coordinates of the i th vertex. PolyL and PolyR are the x coordinates of the left and right sides of the polygon's bounding box. PolyT and PolyB are the y coordinates of the top and bottom. Similarly EdgeL(i), EdgeR(i), EdgeT(i), EdgeB(i) define the bounding box for the i th edge. PointNum is the number of test points. BdryWidth is the "thickness" of the polygon's boundary. It is a tiny fraction of the width of the polygon.
- Lines 8 to 29 are the subroutine Setup. Setup reads in the polygon from the spreadsheet, sets up the bounding boxes described in previous bullet, and generates the random test points and puts them into columns E and F of the spreadsheet.
- Line 23 initializes the Rnd random number function. −1 is the seed. Lines 26 and 27 then generate a sequence of random numbers between 0 and 50.
- Lines 30 to 53 are the subroutine Run. Run applies the entire flowchart shown above to every test point and counts the number of test points inside, outside and on the boundary.
- Lines 54 to 79 are the subroutine Tests. Tests applies the Tests part of the flowchart to one test point.
- Lines 89 to 115 are the subroutine OnTheBorder. OnTheBorder checks if a test point with coordinates (PtX, PtY) is on the boundary of the polygon. It is similar to lines 62 to 65 which test for case (5) except that OnTheBorder is designed to work even if the edge is vertical.
- Min, Max, BBoxPoly and BBoxEdges set up the minimum bounding boxes for the polygon and each of its edges.
If you would like to leave a comment or ask a question please send me an email!