MathOnWeb.com



Appendix 1 - UFOO

UFOO is an acronym for a useful form of one. It is a fraction whose value is 1 because the numerator and the denominator have the same value (even though they may look different). Multiplying an expression by a UFOO does not change the value of the expression but it does change its appearance. Here are some examples that use UFOOs:



Example 1: If we want to express 5 as a multiple of π then we multiply it by the UFOO π/3.14. Then we divide 5 by 3.14 but leave the π symbol alone.



Example 2: If we want to add the common fractions 1/24 and 1/30 the first step is to multiply the first fraction by the UFOO 5/5 and the second fraction by the UFOO 4/4. The result is equivalent fractions with common denominators which can then be added.:



Example 3: To convert between degrees and radians we can use one of these UFOOs:
If we want to convert, say, 118° to radians then we use the one that causes degrees to cancel out (and this time we include the numerical value of π in the division).



Example 4: The following three expressions have very particular denominators:

These binomial denominators have so-called conjugates which are gotten by flipping the sign of the imaginary unit i, or of the radical, or of the sine or cosine. Here is what happens when we choose the conjugate of the denominator to make the UFOO:


In this case the imaginary unit i moves from the denominator to the numerator:


In this case the radical moves from the denominator to the numerator:


In this case the binomial disappears from the denominator and its conjugate appears in the numerator:



Example 5:

This example (and the next one) ask us to prove an identity. We have two expressions that we want to prove are equivalent. Even though there is an = sign we should not think of it as an equation. For instance we CANNOT prove an identity by applying the same operation to both sides. We MUST prove it by manipulating the left-hand-side expression (LHS) into some form and then manipulating the right-hand-side expression (RHS) into the same form.

Suppose that we want to prove the identity

Then we can multiply the LHS by the UFOO −1/−1. The numerator and denominator are separately multiplied by −1 and separately simplified:



Example 6: A UFOO is essential is in the proof of this trigonometric identity.

The problem is that the LHS is a fraction but the RHS is not. We can change the RHS into a fraction if we multiply it by the following UFOO which is chosen so that the denominators on the LHS and RHS match.

Here is what happens to the RHS. We see that after several algebraic manipulations (including using Pythagoras’ theorem ) it is the same fraction as the LHS, thus proving the identity.








Appendix 2 - The equation of the straight line

Suppose that we have the graph of a straight line and that we wish to find its equation. We'll assume that the axes are called x and y and that their scale is linear (not something else, like logarithmic). The equation can be expressed in several possible forms. To find the equation of the straight line in any form we must be given either

      •   two points (x1, y1) and (x2, y2) on the line
or
      •   one point (x1, y1) on the line and the slope m
or
      •   the y intercept b and the slope m.

In the first case where we are given two points, we can find m by using the formula:
Once we have one form we can easily get any of the other forms from it using simple algebraic manipulations. Here are the forms:


1. The slope-intercept form:
y = m x + b.
The constant b is simply the y intercept of the line, found by inspection. The constant m is the slope, found by picking any two points (x1, y1) and (x2, y2) on the line and using the formula:


2. The point-slope form:
y − y1 = m (x − x1).
(x1, y1) is a point on the line. The slope m can be found from a second point, (x2, y2), and using the formula:


3. The general form:
a x + b y + c = 0.
a, b and c are constants. This form is usually gotten by manipulating one of the previous two forms. Note that any one of the constants can be made equal to 1 by dividing the equation through by that constant.



4. The parametric form:
x = x1 + t
y = y1 + m t
This form consists of a pair of equations; the first equation gives the x coordinate and the second equation gives the y coordinate of a point on the line as functions of a parameter t. (x1, y1) is a known point on the line and m is the slope of the line. Each value of t gives a different point on the line.

For example when t = 0 then we get the point
x = x1
y = y1
or the ordered pair (x1, y1), and when t = 1 then we get the point
x = x1 + 1
y = y1 + m
or the ordered pair (x1 + 1, y1 + m), and so on.


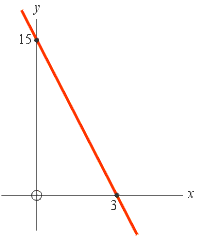Example: Show all of these forms for the straight line shown to the right.

Solution: Two points on this line are (x1, y1) = (0, 15) and (x2, y2) = (3, 0). Thus the y intercept is
b = 15
and the slope is
= −5
1. To get the slope-intercept form,   y = m x + b, we simply substitute in the two values m = −5 and b = 15:
y = −5 x + 15.

2. To get the point-slope form,   y − y1 = m (x − x1), we could use the point (0, 15) as “the” point together with m = −5:
y − 15 = −5 (x − 0)       or simplifying:       y − 15 = −5 x.
Or we could instead use the other point, (3, 0) and get:
y − 0 = −5 (x − 3)       or simplifying:       y = −5 (x − 3).

3. To get the general form,   a x + b y + c = 0, take any of these three forms found so far and distribute and collect all terms on the left-hand-side. The result is the same for all:
5 x + y −15 = 0.
Note that dividing both sides by, say 5, results in the equation
x + 0.2 y − 3 = 0,
which is also in general form and is equivalent in every way to the previous one.


4. To get the parametric form,
x = x1 + t
y = y1 + m t
we could use the point (0, 15) as “the” point together with m = −5:
x = 0 + t
y = 15 −5 t
With this choice, when t = 0 we are at the point (0, 15) and when t = 3 we are at the point (3, 0). We could instead use the other point, (3, 0) and get another parametric form:
x = 3 + t
y = 0 −5 t
With this choice, when t = 0 we are at the point (3, 0) and when t = −3 we are at the point (0, 15). With either choice we will get all the points on the line as we let t range through all values.







Appendix 3 - CAST

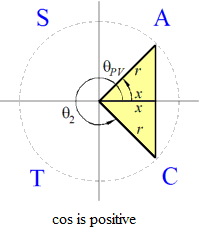
The CAST (or ASTC or unit circle) method is used to find the two angles having a given sine, cosine or tangent.

In this method you draw a set of axes and label the quadrants 1, 2, 3 and 4 with the letters A, S, T and C, respectively, as shown in the diagrams below. The letters mean:
  • A: all three functions, sine, cosine and tangent are positive in this quadrant
  • S: only the sine function is positive in this quadrant
  • T: only the tangent function is positive in this quadrant
  • C: only the cosine function is positive in this quadrant
Next you draw two triangles in standard position on the diagram. The two triangles are congruent (identical) and must be drawn in the two quadrants that have the correct sign for your function. The various diagrams below show all the possible combinations. Make sure that you understand each of them. Then you use your calculator to get the first angle, θPV , and finally you use the symmetry of the diagram to get the second angle, θ2 .


CAST diagrams for the sine function

                




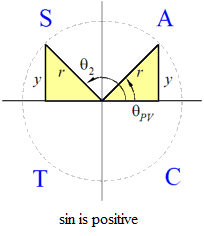
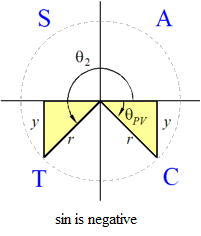
CAST diagrams for the cosine function

                




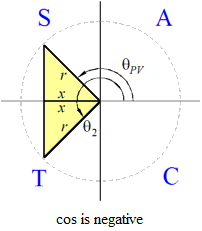
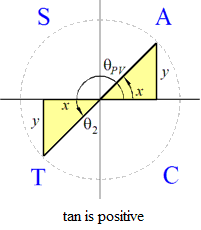
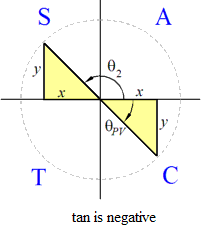
CAST diagrams for the tangent function

                



Example: Find the two angles θ between 0° and 360° for which cos(θ) = −0.4.
  • The CAST diagram for negative cosine is as shown.

  • In degree mode the calculator or Algebra Coach gives

    θPV  = arccos(−0.4) = 113.6°

  • The symmetry of the diagram gives

    θ2  = 360° − 113.6° = 246.4°
Thus the answers are 113.6° and 246.4°.


Example: Find the two angles θ between 0 and 2π radians for which tan(θ) = −3.8.
  • The CAST diagram for negative tangent is as shown.

  • The calculator or Algebra Coach gives

    θPV  = arctan(−3.8) = −1.313 radians

  • The symmetry of the diagram gives

    θ2  = −1.313 + π = 1.828 radians

Because we want answers between 0 and 2π we ‘correct’ θPV  by adding 2π (to get 4.97) and state that the answers are 1.828 radians and 4.97 radians







Appendix 4 - Algorithms for calculating the built-in functions

Algorithms for calculating the following eleven functions are built in to the computer chips used by most scientific calculators and by the Algebra Coach:
sine
(sin)		 cosine
(cos)		 tangent
(tan)
arcsine
(arcsin)		 arccosine
(arccos)		 arctangent
(arctan)
base 10 logarithm
(log)		 natural logarithm
(ln)		 exponential with base e
(exp or e x )
square root
(sqrt)		 power
( y x )

This section explains the algorithms. Studying the algorithms is educational because you learn a lot about the symmetries, identities and other properties of the functions and how they are exploited to make accurate evaluations of the functions.


Algorithm for calculating sin (x)

This algorithm makes it possible for the sine of any angle to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to use a polynomial approximation (step 4) to calculate the sine an angle x. But because this approximation is only accurate for small x we must take steps (1 to 3) to reduce x to the smallest angle that still has the same value of the sine function.
  1. Use periodicity: If x is in the range 0≤x≤360° then go on to step 2. Otherwise, reduce x so that it lies in the range 0≤x≤360° by adding or subtracting a suitable multiple of 360° from it (we are assuming that angle x is measured in degrees). This new x has the same value of the sine function that the original x has.

  2. Use symmetry: If x is in quadrant 1 then go on to step 3. Otherwise if it is in quadrant 2 call it x2, if it is in quadrant 3 call it x3, and if it is in quadrant 4 call it x4.

    The graph shows that four angles: x, x2, x3, and x4, all have the same value of the sine function (except for a − sign.) Thus instead of calculating the sine of x2, x3, or x4 we can calculate the sine of x (the red one in quadrant 1) and just attach a − sign to the answer if the angle was in quadrant 3 or 4. Here are some examples. In each case the quadrant 1 angle is found by using the symmetry of the sine function:

    • sin (110°) = sin (70°)
    • sin (200°) = − sin (20°)     ← attach a − sign
    • sin (330°) = − sin (30°)     ← attach a − sign

  3. Use the cofunction: The argument x has now been reduced to be between 0° and 90°. If it is smaller than 45° then go on to step 4. Otherwise it can be made even smaller by using the following trick: instead of calculating sin(x) we calculate cos(90° − x). This picture shows why we can replace the sine of a big angle, B, by the cosine of a small angle, S:

         
    Set x to the small angle S. Angle x is now small enough to apply the polynomial approximation. Click here to use the cosine polynomial, or proceed to step 4 to use the sine polynomial.

  4. Use the sine polynomial: If angle x is in degrees then convert it to radians by multiplying it by π/180. Then substitute x into the formula:
    For x ≤ π/4 radians (i.e. 45°) this polynomial is accurate to within ±0.00004.


Example: calculate sin (565°). Here are the steps
  1. = sin (205°)       ← use the periodicity of the sin function
  2. = − sin (25°)       ← use the symmetry of the sin function
  3. nothing to do; the argument is already less than 45°
  4.       ← 25° = 0.4363 radians

Example: calculate sin (1.830 radians). Here are the steps
  1. nothing to do; the argument is already between 0 and 2π radians
  2. = sin (1.312)       ← use the symmetry of the sin function
  3. = cos(0.2592)       ← use the cofunction because the argument was greater than 45°
  4.       ← use the cosine polynomial

Algorithm for calculating cos (x)

This algorithm makes it possible for the cosine of any angle to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to use a polynomial approximation (step 4) to calculate the cosine an angle x. But because this approximation is only accurate for small x we must take steps (1 to 3) to reduce x to the smallest angle that still has the same value of the cosine function.
  1. Use periodicity: If x is in the range 0≤x≤360° then go on to step 2. Otherwise, reduce x so that it lies in the range 0≤x≤360° by adding or subtracting a suitable multiple of 360° from it (we are assuming that angle x is measured in degrees). This new x has the same value of the cosine function that the original x has.

  2. Use symmetry: If x is in quadrant 1 then go on to step 3. Otherwise if it is in quadrant 2 call it x2, if it is in quadrant 3 call it x3, and if it is in quadrant 4 call it x4.

    The graph shows that four angles: x, x2, x3, and x4, all have the same value of the cosine function (except for a − sign.) Thus instead of calculating the cosine of x2, x3, or x4 we can calculate the cosine of x (the red one in quadrant 1) and just attach a − sign to the answer if the angle was in quadrant 2 or 3. Here are some examples. In each case the quadrant 1 angle is found by using the symmetry of the cosine function:

    • cos (110°) = − cos (70°)     ← attach a − sign
    • cos (200°) = − cos (20°)     ← attach a − sign
    • cos (330°) = cos (30°)

  3. Use the cofunction: The argument x has now been reduced to be between 0° and 90°. If it is smaller than 45° then go on to step 4. Otherwise it can be made even smaller by using the following trick: instead of calculating cos(x) we calculate sin(90° − x). This picture shows why we can replace the cosine of a big angle, B, by the sine of a small angle, S:

         
    Set x to the small angle S. Angle x is now small enough to apply the polynomial approximation. Click here to use the sine polynomial, or proceed to step 4 to use the cosine polynomial.

  4. Use the cosine polynomial: If angle x is in degrees then convert it to radians by multiplying it by π/180. Then substitute x into the formula:
    For x ≤ π/4 radians (i.e. 45°) this polynomial is accurate to within ±0.000004.


Example: calculate cos (565°). Here are the steps
  1. = cos (205°)       ← use the periodicity of the cosine function
  2. = − cos (25°)       ← use the symmetry of the cosine function
  3. nothing to do; the argument is already less than 45°
  4.       ← 25° = 0.4363 radians

Example: calculate cos (1.830 radians). Here are the steps
  1. nothing to do; the argument is already between 0 and 2π radians
  2. = −cos (1.312)       ← use the symmetry of the cosine function
  3. = −sin(0.2592)       ← use the cofunction because the argument was greater than 45°
  4.       ← use the sine polynomial

Algorithm for calculating tan (x)

This algorithm makes it possible for the tangent of any angle to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to use a polynomial approximation (step 5) to calculate the tangent an angle x. But because this approximation is only accurate for small x we must take steps (1 to 4) to reduce x to the smallest angle that still has the same value of the tangent function.
  1. Use periodicity: If x is in the range 0≤x≤180° then go on to step 2. Otherwise, reduce x so that it lies in the range 0≤x≤180° by adding or subtracting a suitable multiple of 180° from it (we are assuming that angle x is measured in degrees). This new x has the same value of the tangent function that the original x has.

  2. Use symmetry: If x is in quadrant 1 then go on to step 3. Otherwise it is in quadrant 2, in which case we will call it x2. The graph shows that, except for a − sign, x and x2 have the same value of the tangent function. Thus instead of calculating the tangent of x2 we can calculate the tangent of x (the red one in quadrant 1) and just attach a − sign to the answer.

    The quadrant 1 angle is found by using the symmetry of the tangent function. For example tan (110°) = − tan (70°).

  3. Use the cofunction: The argument x has now been reduced to be between 0° and 90°. If it is smaller than 45° then go on to step 4. Otherwise it can be made even smaller by using the following trick: instead of calculating tan(x) we calculate tan(90° − x) and take the reciprocal. This picture shows why we can replace the tangent of a big angle, B, by the reciprocal of the tangent of a small angle, S:

         
    Set x to the small angle S. x is now less than 45°.

  4. Use a trigonometric identity: If x is less than 22.5° then go on to step 5. Otherwise use this trig identity:
    to replace a calculation of the tangent of some angle by a calculation involving an angle that is half as big. The argument of the tangent function is now less than 22.5°.

  5. Use the polynomial: If angle x is in degrees then convert it to radians by multiplying it by π/180. Then substitute x into the formula:
    For x ≤ π/8 radians (i.e. 22.5°) this polynomial is accurate to within ±0.000006.


Example: calculate tan (194°). Here are the steps
  1. = tan (14°)       ← use the periodicity of the tangent function
  2. nothing to do; the argument is already between 0 and 90°
  3. nothing to do; the argument is already between 0 and 45°
  4. nothing to do; the argument is already between 0 and 22.5°
  5.       ← 14° = 0.2443 radians

Example: calculate tan (110°). Here are the steps
  1. nothing to do; the argument is already between 0 and 180°
  2. = − tan (70°)       ← use the symmetry of the tangent function
  3. = − 1 / tan(20°)       ← use the “cofunction” because the argument was greater than 45°
  4. nothing to do; the argument is already less than 22.5°
  5.       ← 20° = 0.3491 radians

Example: calculate tan (40°). Here are the steps
  1. nothing to do; the argument is already between 0 and 180°
  2. nothing to do; the argument is already between 0 and 90°
  3. nothing to do; the argument is already between 0 and 45°
  4. use the trig identity
  5. Calculate the polynomial for tan (20°) using 20° = 0.3491 radians:
    and substitute the result into the trig identity of step 4:

Algorithm for calculating arctan (x)

This algorithm makes it possible for the arctangent of any number to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to to use a polynomial approximation (step 4) to calculate the arctan(x). But because this approximation is only accurate for small arguments x we must take several steps (1 to 3) to reduce x to a smaller value. We assume that the desired output of the arctangent function is an angle in radians.
  1. Use symmetry: If the argument x is positive then go on to step 2. Otherwise use the fact that arctan(−x) = −arctan(x) to make the argument positive.

  2. Use the complementary angle: If the argument x is less than 1 then go on to step 3. Otherwise use the fact that:
    to replace the arctangent of a value bigger than 1 by the arctangent of a value smaller than 1. This equation follows from the fact that angles B and S in the triangle shown are given by:

         

    and that .

  3. Use an identity: If x ≤ (about 0.268) then go on to step 4. Otherwise use the identity:
    to replace the arctangent of a value x bigger than by the arctangent of a value smaller than .

  4. Use the polynomial: Substitute the argument x into the formula:
    For x ≤ (about 0.268) this polynomial gives an angle in radians that is accurate to within ±0.00002. To convert this angle to degrees multiply it by 180/π.


Example: Calculate arctan (0.7813) and express the answer in degrees. Here are the steps:
  1. nothing to do; the argument is already positive
  2. nothing to do; the argument is already less than 1
  3. use the identity:
  4. use the polynomial to evaluate the new arctangent:
    Substitute this back into the original arctangent and then convert the answer to degrees:


Algorithms for calculating arcsin (x) and arccos (x)

These algorithms use the algorithm for the arctangent function. Click here to see that algorithm.

arcsine: Consider the triangle shown to the right. Notice that both of the following statements describe the angle θ:
Putting them together we get the equation:
We can use this equation to replace the calculation of the arcsine of some quantity x by the calculation of the arctangent of some related quantity. Click here to see the arctangent algorithm.

arccosine: Look at the triangle again. Notice that both of the following statements describe the angle φ:
Putting them together we get the equation:
We can use this equation to replace the calculation of the arccosine of some quantity x by the calculation of the arctangent of some related quantity. Click here to see the arctangent algorithm.




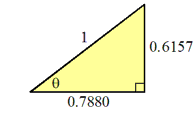
Example: Consider the right triangle shown here.

We can calculate angle θ using the arcsine:
Alternatively we can calculate angle θ using the arccosine:
In either case we have reduced the problem to calculating arctangent. Using the algorithm for calculating the arctangent (given above), this becomes:


Algorithm for calculating log (x)

This algorithm makes it possible for the base 10 logarithm (log) of any positive number to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to to use a polynomial approximation (step 4) to calculate log(x). But because this approximation is only accurate for small arguments x we must take several steps (1 to 3) to reduce x to a smaller value.
  1. Express the number x in scientific notation:   x = m · 10 p.   Then
    log (x) = log (m) + p,
    where p is an integer and m (the new argument of the base 10 logarithm function) is a number between 1 and 10.

  2. Use the square root: Use the fact that:
    to reduce the argument of the base 10 logarithm function even further, to a value between 1 and .

  3. Replace log by ln: Use the change of base formula:
    log (x) = 0.43429448 ln (x)
    (This follows from the fact that 1 / ln (10) = 0.43429448). Putting steps 1, 2 and 3 together gives:
  4. Use the polynomial: For any argument x between 1 and , the following polynomial:
    where , accurately gives ln (x) to within ±0.0008.


Example: Calculate log (900). Here are the steps:
  1. 900 = 9 · 10 2  so  log (900) = log (9) + 2
  2. log (900) = 2 log (3) + 2
  3. log (900) = 0.86858896 ln (3) + 2
  4. use the polynomial to evaluate ln (3).
    x = 3 gives y = 2/4 = 0.5 so the polynomial becomes:
    Substitute this back into the result from step 3:
    log (900) = 0.86858896 · 1.098 + 2 = 2.954


Algorithm for calculating ln (x)

This algorithm makes it possible for the natural logarithm (ln) of any positive number to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to to use a polynomial approximation in step 3 to calculate ln (x). But because this approximation is only accurate for small arguments x we must take steps 1 and 2 to reduce x to a smaller value.
  1. Express the number x in scientific notation:   x = m · 10 p.   Then
    ln (x) = ln (m) + 2.3025851 p,
    where p is an integer and m (the new argument of the natural logarithm function) is a number between 1 and 10.
    (Note that ln (10) = 2.3025851)

  2. Use the square root: Use the fact that:
    to reduce the argument of the natural logarithm function even further, to a value between 1 and .
    Putting steps 1 and 2 together gives:
  3. Use the polynomial: For any argument x between 1 and , the following polynomial:
    where , accurately gives ln (x) to within ±0.0008.


Example: Calculate ln (9000). Here are the steps:
  1. 9000 = 9 · 10 3  so  ln (9000) = ln (9) + 3 · 2.3025851
  2. ln (9000) = 2 · ln (3) + 3 · 2.3025851
  3. use the polynomial to evaluate ln (3).
    x = 3 gives y = 2/4 = 0.5 so the polynomial becomes:
    Substitute this back into the result from step 2:
    ln (9000) = 2 · 1.098 + 3 · 2.3025851 = 9.104


Algorithm for calculating exp (x) or e x

This algorithm makes it possible for exp (x) or e x to be calculated using only the operations of addition, subtraction, multiplication and division. The basic idea is to to use a polynomial approximation in step 3 to calculate e x. But because this approximation is only accurate for small arguments x we must take steps 1 and 2 to reduce x to a smaller value.
  1. Split up x: Write x = n + r, where n is the nearest integer to x and r is a real number between −½ and +½. Then e x = e n · e r.

  2. Evaluate e n: Multiply the number e by itself n times. To 14 digits, e = 2.7182818284590. The multiplication can be done quite efficiently. For example e 8 can be evaluated with just 3 multiplications if it is written as (((e) 2 ) 2 ) 2. To further increase efficiency various integer powers of e can be calculated once and stored in a lookup table.

  3. Evaluate e r using the polynomial:
    For r between −½ and +½ this polynomial is accurate to within ±0.00003.


Example: Calculate exp (−3.8) or e −3.8 :
  1. Split it into two factors:
  2. Evaluate the first factor using multiplication:
  3. Evaluate the second factor using the polynomial:
    Multiply the two factors to get the answer:


Algorithm for calculating the square root

This algorithm uses Newton's method. It makes it possible for the square root of any positive number to be calculated using only the operations of addition, subtraction, multiplication and division.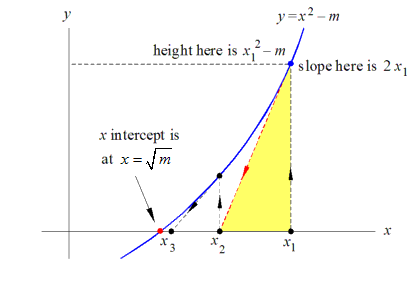

The basic idea is this: if we want to calculate the square root of some number m then we draw a graph of the function y = x 2 − m, as shown in the picture to the right, and find the point where the graph crosses the x axis. This is the red dot at x = .

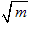Newton's method for finding this point starts with any initial estimate of the square root, indicated by the point x1 in the picture. It uses the height and slope of the of the curve at x1 (the blue dot and the red dashed line) to obtain a better estimate, x2, of the square root. This better estimate is then used to get an even better estimate, x3, and so on. Each iteration (cycle) doubles the number of digits of accuracy of the square root. When two successive estimates of the square root differ by less than some small value, say 0.0001, then the algorithm stops and we have the square root, accurate to within ±0.0001.

Given any estimate x1 of the square root of m we can obtain the improved estimate x2 by using the formula:
This formula is easily derived by solving the equation:
for x2. This equation is just a statement that the slope of the curve at the blue dot (which is derived using calculus) equals the slope of the slanted side of the yellow triangle.



Example: Calculate the square root of 900 accurate to ±0.000001.
Starting with an initial guess of 50 here are the results of the first 6 iterations:
x1 50
x2
x3 30.2352941176471
x4 30.0009155413138
x5 30.0000000139698
x6 30.0000000000000
We have shown the calculation for x2 in detail. We have also shown the 6th decimal place in red. On the 6th iteration there is no change in this decimal place so we can stop and give x6 as the answer. Since we know that the exact answer is 30 we can see how the number of correct digits roughly doubles with every iteration.



Algorithm for calculating the power function

We can use the following equation to replace the calculation of the power function with a calculation of the natural logarithm and the e x function:
This equation follows from the identity e ln (x) = x and the exponention property of exponents.


Example: Evaluate 5.2 3.6








Appendix 5 - Extending the elementary functions to the complex numbers

This section lists the formulas used for evaluating the eleven functions when their arguments or their values are complex numbers. The idea is to replace the expression on the left side of the formula by the expression on the right. This new expression contains only functions of real numbers. (Assume that x = a + b i  is a complex number in rectangular form and that y = r ∠ s = r e i s  is another complex number in polar or exponential form.)
  1. To evaluate exp (x) or e x, where x is complex, use the following formula. The right side contains only evaluations of exp, sin or cos of real numbers:
  2. To evaluate sin (x), where x is complex, use the following formula. The two terms in the numerator on the right side are evaluated using formula # 1:
  3. To evaluate cos (x), where x is complex, use the following formula. The two terms in the numerator on the right side are evaluated using formula # 1:
  4. To evaluate tan (x), where x is complex, use the following formula. The numerator on the right side is evaluated using formula # 2 and the denominator using formula # 3:
  5. To evaluate the square root of a complex number y, first express y in polar form, and then use this formula:
  6. To evaluate the natural logarithm of a complex number y, first express y in polar form or exponential form, and then use this formula:
  7. To evaluate the base 10 logarithm of a complex number y use the following formula. The numerator on the right side is evaluated using formula # 6:
  8. To evaluate the power function, y x, where x and y are complex, first express y in polar form or exponential form and then use the following formula. Click here to see an example:
  9. To evaluate the arcsin of a complex number a + b i use this formula:
    where
    and
  10. To evaluate the arccos of a complex number a + b i use this formula:
    where A and B are the same as for formula # 9.

  11. To evaluate the arctan of a complex number a + b i use this formula: