MathOnWeb.com

Finding Areas Using the Monte Carlo Method

The Monte Carlo Method gets its name from the city of Monte Carlo and the games of chance that are played in the casinos there. In mathematics this name is used whenever a problem is solved by a method that uses random numbers. The Monte Carlo method has been used in the following situations:

1. in computer simulations of processes that involve some element of randomness, such as the diffusion of neutrons out of a nuclear reactor or customers arriving at a queue,
2. in computer games to decide what the computer-generated characters in the game will do next,
3. in calculating the areas of irregular shapes.

Finding Areas: It is generally very difficult to find the area of an irregular shape such as the one shown to the right. We will show how it can easily be done using the Monte Carlo Method. Click here if you want to see some other methods first.

Here are the steps to the Monte Carlo method:

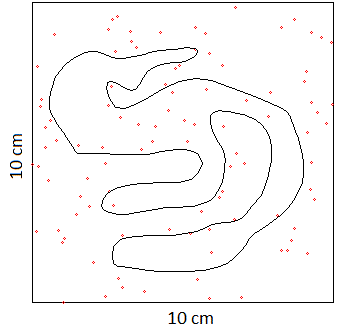
1. Put the object inside a rectangle of given area. Suppose that this rectangle has an area of 100 cm².
2. Place a given number of points, say 100, at random locations inside the rectangle.
3. Count the number of random points that lie inside the object.
   
4. The area of the object is proportional to the number of points that lie inside it and is given by this formula:
   

   If you count you will find that 22 points lie inside the object. Thus our estimate of the area is:

   
   
   
5. If we add another 900 points at random inside the rectangle (for a total of 1000) we get an improved estimate of the area. We now find that 280 points lie inside the object. This puts the area of the object at:

Note on each step:

1. One advantage of the Monte Carlo method is that it can easily be generalized to multi-dimensional integrals. For example we could find the volume of a solid by putting it inside a cube of a given volume.
2. The coordinates of the random points are generated by successive calls to a random number generator that generates real numbers uniformly between 0 and 10.
3. To count the points inside the shape seems simple to the human brain but is not so easy for the computer. This is called the Inside / Outside Problem.
4. For maximum efficiency make the bounding rectangle as small as possible so more points end up inside the shape.
5. Accuracy improves with each random point added but unfortunately the accuracy is only proportional to the square root of the number of points. This means that to improve the accuracy by a factor of 10 requires 100 times as many points.