MathOnWeb - Pinball and Pascal's Triangle

The Pinball Machine

The picture to the right shows a type of pinball machine that you can build yourself. You will need 10 nails, 5 small cups, a wooden board and a pinball (marble). Nail the nails part way into the board in the triangular pattern shown, with one nail in the top row, two in the second row, three in the third row and so on, and with enough space for the pinball to fit between the nails.

To operate the machine release the pinball so that it hits the top nail dead center. The pinball will be deflected either left or right with equal probability by the first nail. It will then continue falling and hit one of the nails in the second row and be deflected either left or right around that nail with equal probability, and so on.

The result is that the pinball follows a random path, deflecting off one pin in each of the four rows of pins, and ending up in one of the cups at the bottom. The various possible paths are shown by the gray lines and one particular path is shown by the red line. Click here to see an animation of a similar machine called the Galton Box.

Let's describe the path shown in red using the notation "LRLL" meaning "deflection to the left around the first pin, then deflection right around the pin in the second row, then deflection left around the third and fourth pins".

Question: How many different paths are there through the pinball machine and what are they?

Answer: There are 16 different paths through the machine. The list of paths is:

LLLL LLLR LLRL LLRR
LRLL LRLR LRRL LRRR
RLLL RLLR RLRL RLRR
RRLL RRLR RRRL RRRR

Click here for an explanation.

Question: How many paths are there that end up in any given bin?

To answer this question we have to sort the list of the 16 different paths according to how many R's each path contains:

Number of R's = 0: { LLLL }
Number of R's = 1: { LLLR LLRL LRLL RLLL }
Number of R's = 2: { LLRR LRLR LRRL RLLR RLRL RRLL }
Number of R's = 3: { LRRR RLRR RRLR RRRL }
Number of R's = 4: { RRRR }

If the number of R's = 0 then the pinball ends up in the first (leftmost) bin, (1 path leads here)

If the number of R's = 1 then the pinball ends up in the second bin, (4 paths lead here)

If the number of R's = 2 then the pinball ends up in the third bin, (6 paths lead here)

If the number of R's = 3 then the pinball ends up in the fourth bin, (4 paths lead here)

If the number of R's = 4 then the pinball ends up in the last (rightmost) bin, (1 path leads here).

The result is as shown in the picture to the right.

Question: What is the probability that the pinball will end up in any given bin?

There are 16 paths and each path is equally likely so each path has a 1 in 16 chance of being followed. Thus the probabilities are:

probability = 1/16 to end up in first (leftmost) bin
probability = 4/16 to end up in second bin
probability = 6/16 to end up in third bin
probability = 4/16 to end up in fourth bin
probability = 1/16 to end up in fifth (rightmost) bin

A histogram of these values is shown to the right. If we drop many pinballs through the machine and let them pile up in the bins then over the long run they will be distributed as shown in the histogram to the right. This is an example of the binomial distribution which is studied in probability. The bell curve or normal distribution is based on this distribution.

Pascal's Triangle

The object shown to the right is known as Pascal's Triangle. (Blaise Pascal, its discoverer, was born in France and died in 1662 at the age of 39. The Pascal programming language is named after him.)

Pascal's triangle is very useful for analysing the pinball machine. Pascal's triangle also pops up in a variety of other seemingly unrelated areas, as we shall soon see.

First we mention that Pascal's triangle continues on forever and we have only shown the first 5 rows. Can you see the pattern and guess what the next row of numbers is?

The next row is shown in the animation to the right. The pattern for each row of the triangle is:

the left and right ends always equal 1
each internal element is the sum of the two elements above left and above right, like this:

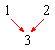
If we superimpose Pascal's triangle on top of the pinball machine then we can see a connection between the two: Each number of Pascal's triangle is equal to the number of distinct paths that a pinball can take to arrive at that point in the pinball machine. (The very way the pinball machine is constructed guarantees this: Any point on the left edge can only be reached by 1 path and the same for any point on the right edge. Any interior point can only be reached from the above-left point or the above-right point, so adding their path numbers together gives the number of paths leading to the interior point.)

The problem with this method of constructing Pascal's triangle is that to get the numbers for any given row we must construct all the rows above it.

But there is another way to get all the numbers in Pascal's triangle at once. To do it we must think of the various paths through the pinball machine as arrangements of L's and R's. The mathematics of arrangements involves factorials, permutations and combinations. Click here to learn about those.

Factorial

When we are counting arrangements of objects a certain type of multiplication appears over and over again, so it is useful to define the factorial.

Definition: The factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n.

Thus 3 × 2 × 1 can be written as 3! and is spoken as "three factorial". Look for the factorial function on your calculator. Here are more examples:

5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3628800
69! = 69 × 68 × … × 3 × 2 × 1 = 1.71x10⁹⁸ (the biggest factorial my calculator can display)

As you can see factorials get very big very fast. The reason that the number n is a non-negative integer is that it is a number of objects and that is a whole number. And since we could have zero objects we also define 0!. It doesn't fit the pattern so we simply define it to equal 1.

Permutations

Suppose that we want to put 3 books in a bookshelf. How many different ways can they be arranged from left to right?

The answer is 6 ways. If we call the books A, B, C then the possible arrangements are:

ABC, ACB, BAC, BCA, CAB and CBA

This can be understood by looking at the tree diagram. Starting at the left, there are 3 branches meaning that there are 3 choices for the first (leftmost) book: A, B or C. Moving to the next (middle) book we have two choices because the first book has already been placed. Moving to the final (rightmost) book we have only one choice because all the other books have already been placed. Multiplying 3 branches × 2 branches × 1 branch gives 3! or 6 branches or arrangements or permutations.

Definition: A permutation of a set is an arrangement of its members into a sequence, or if the set is already ordered, a rearrangement of its members. The number of possible permutations of n objects is n!.

Question: Suppose that we have 8 books in a bookshelf and we only have time to read 2. So we select 2 books at random. The first book selected will be read first (this is important) and the second one selected will be read second. How many different outcomes are possible?

Answer: 8 × 7 or 56 outcomes. To see this make a tree with 8 branches describing the 8 possibilities for the first book selected. At the end of every branch put 7 branches describing the 7 possibilities for the second book selected. The result is 56 branches.

If two of the books in the bookshelf are called A and B then one of these 56 outcomes is AB and another one is BA. They are different outcomes because in one outcome book A is read first and in the other outcome book B is read first. These 56 arrangements are called partial permutations – partial because we do not select all the books, and permutation because selecting in a different order counts as a different outcome.

It is useful to write 8 × 7 in terms of canceling factorials and in terms of a new function called P, like this:

Think of ₈P₂ as being the same as 8! but keeping only the two biggest factors. Look for the P function on your calculator. In general:

Definition: The permutation function _nP_k counts the number of possible arrangements of k items selected from n objects.

Combinations

Suppose that we have 3 people, call them A, B and C, and we want to select 2 of them at random to work together on a project. So we put the 3 names in a hat and randomly select 2 names. This is similar to a partial permutation problem with ₃P₂ = 6 possible outcomes as shown in the tree diagram – but there is a difference. We don't care about the order. Selecting A, then B is the same as selecting B, then A. Thus the number of outcomes should be cut in half. The number of possible combinations or teams is 3. They are:

{A and B}, {A and C}, {B and C}

In general if the order of selection doesn't matter then we must correct the number of outcomes given by the P function by dividing it by the number of ways that the selected items can be permuted. This is the job of the combination function C.

Definition: A combination is a selection of k items from a set that has n members, such that the order of selection does not matter (unlike permutations where the order does matter).

Definition: The combination function _nC_k counts the number of possible combinations of k items selected from a set of n members.

If you clicked the link above then you learned about combinations and the combination function:

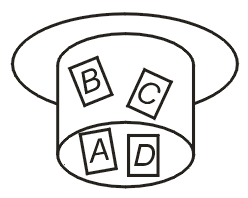
Typical combination question: Suppose that we have 4 people, call them A, B, C and D, and we want to select 2 of them at random to work together on a project. So we put the 4 names in a hat and randomly select 2 names. We don't care about the selection order – selecting A, then B is the same as selecting B, then A. How many different outcomes are there and what are they?

Answer: This is a combination problem because the selection order does not matter. The set consists of n=4 members and we are selecting k=2 of them. The combination function gives

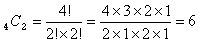
So the number of possible combinations or teams is 6. They are:

{A and B}, {A and C}, {A and D}, {B and C}, {B and D}, {C and D}.

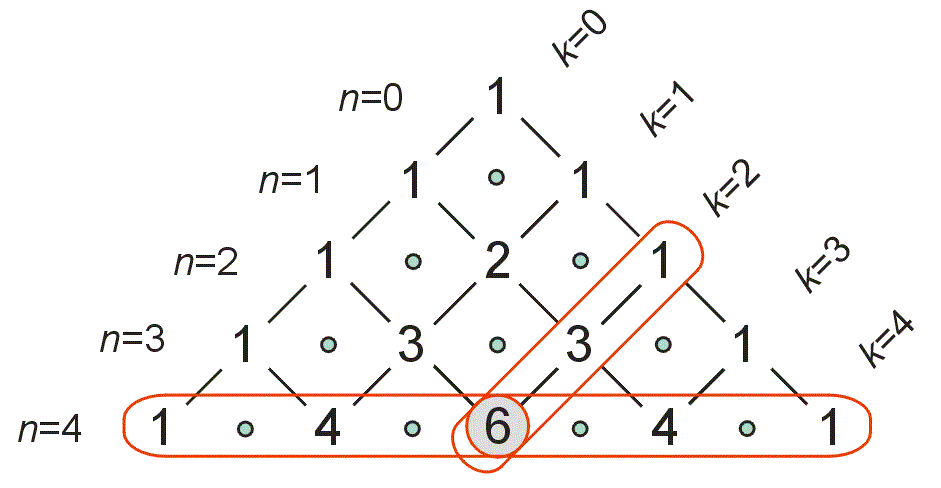
To see how combinations can describe paths in the pinball machine consider how a pinball can arrive at the point circled in gray. It has to be deflected by 4 pins and it has to go right 2 times. This is just like the combination question above if we put slips of paper with the numbers 1 to 4 in a hat and randomly select 2 slips. Let these slips tell us where we will deflect to the right. For example if we select the numbers 1 and 4 this means we will follow the path RLLR. From the above question we know that there are ₄C₂=6 combinations so this entry in Pascal's triangle should also be 6.

Thus Pascal's triangle is essentially a listing of all the possible values of the combination function!

The Binomial Theorem: It is perhaps surprising that the combination function can be used to expand an expression like (a+b)⁴. Here is the expansion:

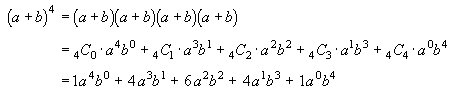
The second row shows how the combination function is involved. It appears here because for example the term a³b comes from multiplying one b from inside one of the brackets and three a's from inside the other three brackets. There are ₄C₁=4 ways of selecting which bracket the b should come from.

The blue arrows show one of these ways:

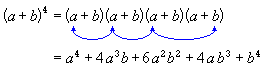
If you would like to leave a comment or ask a question please send me an email!