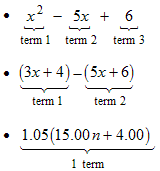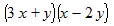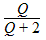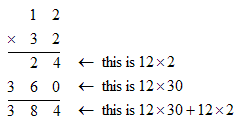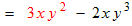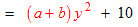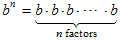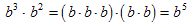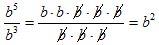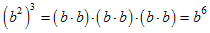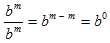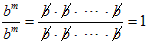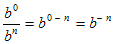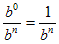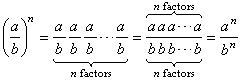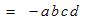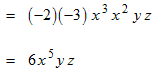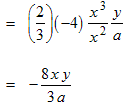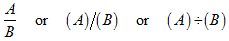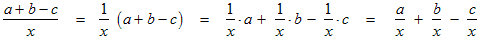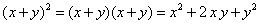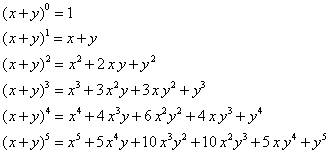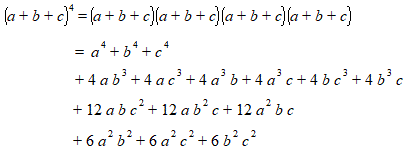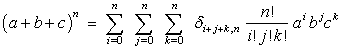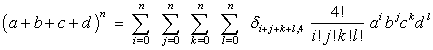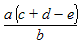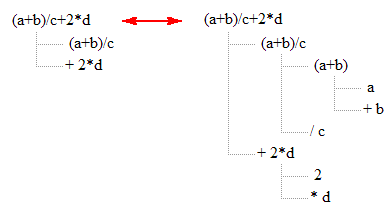Chapter 3 - Expressions
This chapter discusses algebraic expressions. It contains the following sections:- section 3.1 - In this section we introduce expressions, define parts of expression, types of expressions and explain the distributive law.
- section 3.2 - We explain the addition and subtraction of expressions.
- section 3.3 - We give the basic properties of exponents. These properties are required in the following two sections on the multiplication and division of expressions.
- section 3.4 - We explain the multiplication of expressions. There are three cases, depending on whether the expressions are monomials or multinomials.
- section 3.5 - We explain the division of expressions. There are three cases, depending on whether the expressions are monomials or multinomials.
- section 3.6 - We present the binomial and multinomial theorems, which describe how to expand powers of binomials and multinomials.
- section 3.7 - We present a data structure called a tree which holds the structure of an expression.
- section 3.8 - This is a reference section that lists in one place all the simplifications that could possibly be applied to an expression.
3.1 - Introduction to expressions
- What is an expression?
- Evaluating an expression
- The parts and properties of an expression
- Making substitutions and using an alias
- The distributive law
- The distributive law generalized (including the FOIL method)
What is an expression?
A mathematical expression is a set of numbers and letters that represent numbers, combined using mathematical operations such as addition, subtraction, multiplication, division, roots, powers and functions. |
Notice that an = sign is not allowed. Including one would create an equation.
The section “Introduction: Exactly what is algebra?” gave a very nice example of an expression. Here are some other examples of expressions:
- 1.05 (15.00 n + 4.00)
- 170 sin (377 t + 2.4)
- x 2 − 5 x + 6
Evaluating an expression
To evaluate an expression means to assign values to all the letters that represent numbers and then carry out the mathematical operations (obeying the rules for the order of operations) to yield a numerical value for the expression. |
For example if we let n equal 4 in the first expression above, 1.05 (15.00 n + 4.00), then the expression would become 1.05 (15.00 · 4 + 4.00), which simplifies to 67.20, meaning that the customer pays $67.20 for 4 items.
The parts and properties of an expression
Just as a sentence can be broken down in various parts such as subject, verb and object, so a mathematical expression can be broken down into various parts. In this section we define and give examples of the following parts and properties of an expression:Definition: Any letters in an expression that are allowed to change value during the course of a problem are called variables. Any letters that don't change value during a problem (but may change value from one problem to another problem) are called constants. Numbers, of course, are also constants. |
Example: The expression ½ g t 2 describes the distance a falling object has fallen t seconds after it has been released. In a typical problem g is a constant with the value 9.81 and t is a variable to which we assign different values of time. why don 't we just always use the number 9.81 instead of the letter g? Because in a different problem we may want to study objects falling on the moon. The same equation applies; the only difference is that on the moon g has the value 1.6.
Definition: An expression can always be considered to be made up of parts that are added or subtracted together. Those parts are called terms. |
Examples. Notice that the brackets in the second and third expressions cause the number of terms in those expressions to be 2 and 1.
Definition:
|
Examples:
- 5 x 2 y is a monomial
- a + b is a binomial
- x 2 − 5 x + 6
is a polynomial
- x 2.4 − 5 x + 6 is a trinomial (but not a polynomial)
Definition: A monomial or term can always be considered to be made up of parts that are multiplied together. Those parts are called the factors of the monomial. (Click here to review factors of a natural number, on which this is based.) Also, a monomial can always be considered to break into two factors: one factor containing only constants and one factor containing only variables. The constant factor is called the coefficient of the monomial. If there is no constant factor then the coefficient is understood to be 1. |
Examples. In the following examples assume that a is a constant and x and y are variables.
- 5 x ← 5 and x are the factors; 5 is the coefficient
- − x 2 ← − 1
and x 2 are the factors; − 1 is the coefficient
- −5 a x
← −5, a and x
are the factors; −5 a is the coefficient
- x y ← x and y are the factors; 1 is the coefficient
Definition of degree:
|
Examples: In the following examples assume that a and b are constants and x and y are variables.
- 5 x 2 has degree 2.
- 5 x 2 y has degree 3.
- a x + b has degree 1.
- x 2 − 5 x + 6
has degree 2.
Definition: Like terms are terms that differ only in their coefficients; they have identical variable factors. In the next section, 3.2, we will see that like terms can be added by adding their coefficients. |
Examples: Assume that x and y are variables. The like terms are shown in red.
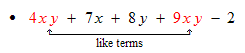
The coefficients of the like terms are 4 and 9. 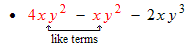
The coefficients of the like terms are 4 and − 1. 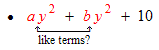
If a and b are constants then the indicated terms ARE like terms and a and b are the coefficients. If a and b are variables then the indicated terms are NOT like terms.
Making a substitution and using an alias
Making a substitution means replacing a variable in an expression with a given expression. |
This is similar to evaluating an expression except that you substitute in an expression rather than a number. It is usually necessary to put brackets around the substituted expression to preserve the proper order of operations.
Example 1: Substitute 2 x + y for the variable t in the expression t 2 + 9.
(2 x + y) 2 + 9
Example 2: Typing
A = 3 x + y, B = x − 2 y, A Binto the Algebra Coach program and clicking on the Substitute button will substitute 3 x + y in for the variable A and x − 2 y in for the variable B in the expression A B. The result is:
In mathematics an alias is a single symbol (usually a capital letter like Q, short for the word Quantity) that represents a given expression. Using an alias means replacing the given expression by the alias wherever the given expression occurs inside another expression. An alias is usually used to make an expression look simpler and allow one not to be distracted by details. |
Example: Consider the expression
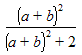 Let us use the alias Q = (a + b) 2.
Then the expression becomes:
Let us use the alias Q = (a + b) 2.
Then the expression becomes:
The distributive law
|
Let a, b and c be any numbers. The distributive law states that: a (b + c) = a · b + a · c expanding → ← factoringIf we convert the expression on the left to the expression on the right then we say that we are distributing or expanding the expression. (Distributing because we are handing out or distributing a factor of a to each term in the brackets. Expanding because we are replacing an expression with one term by one with two terms.) On the other hand, if we convert the expression on the right to the expression on the left then we say that we are factoring the expression (because the new expression is a product of factors). |
We use the distributive law all the time in everyday life. For example when we add $9 and $8 to get $17 we are factoring using the distributive law:
$9 + $8 = $(9+8) = $17(Not convinced? Try adding $9 and 8¢ and see if you get 17 of anything!)
As another example, suppose we multiply 12 times 32 using long multiplication:
This is just a tabular way of doing this:
12 · 32 = 12 · (30 + 2) = 12 · 30 + 12 · 2 = 360 + 24 = 384We are expanding using the distributive law at the step with the red = sign.
The distributive law generalized
The basic distributive law, a (b + c) = a b + a ccan be generalized in many useful ways. We present four variations of the left side and show how the right side changes as a result. 1. The multinomial factor (b + c) on the left side can actually have any number of terms and the monomial factor a simply distributes over all of them. (Click here for the proof.) For example: a (b + c + d + e) = a b + a c + a d + a e 2. The multinomial factor on the left side can have terms that are subtracted instead of added. The result is that on the right side the corresponding terms are also subtracted. (Click here for the proof.) For example: a (b − c − d + e) = a b − a c − a d + a e 3. The monomial factor on the left side can be negative. The result is that on the right side the terms have their signs reversed. (Click here for the proof.) For example: −a (b − c − d + e) = − a b + a c + a d − a eA special case is when the monomial factor on the left side is −1, in which case we don't have to write the “1” factor and can simply write: − (b − c − d + e) = − b + c + d − e 4. The left side can be the product of two multinomials. Each term of the first multinomial distributes onto each term of the second multinomial. Probably the most important example is the product of 2 binomials: (a + b) (c + d ) = a c + a d + b c + b d(Click here for the proof.) Some people use the acronym FOIL (First, Outer, Inner, Last) to remember what terms on the left side are multiplied to give each of the four terms on the right side. F = first term from each factor, O = outer terms of the factors, I = inner terms of the factors, L = last term from each factor. |
| F O I L: This picture shows how each term of the first factor distributes onto each term of the second factor. Match an arc with a term of the same color. | 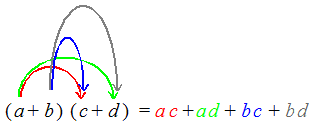
|
Proof that: a (b + c + d + e) = a b + a c + a d + a e
a (b + c + d + e) ← start with the left side = a (b + Q) use the alias Q = c + d + e = a b + a Q use the distributive law = a b + a (c + d + e) substitute back for Q and repeat the above process until there is nothing left to distribute = a b + a c + a d + a e the final result is the right side
Proof that: a (b − c − d + e) = a b − a c − a d + a e
a (b − c − d + e) ← start with the left side = a (b + (−c) + (−d ) + e) change subtraction to addition of a negative = a b + a (−c) + a (−d ) + a e use the generalized distributive law proved just previous = a b + (−a c) + (−a d ) + a e use the fact that a positive times a negative is negative = a b − a c − a d + a e change the addition of a negative back into subtraction; the final result is the right side
Proof that: −a (b − c − d + e) = − a b + a c + a d − a e
−a (b − c − d + e) ← start with the left side Q (b − c − d + e) use the alias Q = −a = Q b − Q c − Q d + Q e use the generalized distributive law proved just previous = (−a) b − (−a) c − (−a) d + (−a) e substitute back for Q = (−a b) − (−a c) − (−a d) + (−a e) use the fact that a negative times a positive is negative = − a b + a c + a d − a e use the fact that adding a negative is subtracting and subtracting a negative is adding; the final result is the right side
Proof that: (a + b) (c + d ) = a c + a d + b c + b d
(a + b) (c + d ) ← start with the left side = Q (c + d) use the alias Q = (a + b) = Q c + Q d use the distributive law = (a + b) c + (a + b) d substitute back for Q and distribute again = a c + b c + a d + b d the result, after rearranging the terms, is the right side
3.2 - Addition and Subtraction of Expressions
Before studying this topic you may wish to review the section on addition and subtraction of numbers.Suppose that A and B are any two expressions. Adding B to A means setting up the sum as
(A) + (B),and then simplifying as much as possible. Subtracting B from A means setting up the difference as
(A) − (B),and then simplifying as much as possible.
The reason that we put brackets around A and B is that they are expressions, not just numbers, and the addition or subtraction is supposed to apply to whatever A and B may contain. (We want the addition or subtraction to be at the end in the order of operations.)
The simplifications that must be done are:
Example: If A = 4 x y + 7 and B = 8 y + 9 x y then setting up the sum A + B gives:
(4 x y + 7) + (8 y + 9 x y)and setting up the difference A − B gives:
(4 x y + 7) − (8 y + 9 x y)
Removing the brackets
Removing the brackets from (A) + (B) is easy:(A) + (B) always simplifies directly to A + B. The brackets can just be dropped. |
Here’s why: The acronym BEDMAS (Brackets, Exponents, Division and Multiplication, Addition and Subtraction) helps us remember the order of operations within an expression. Brackets are at the top of the priority list and addition and subtraction are at the bottom.
In the expression A + B the addition is already at the bottom of the list so we don’t need brackets around A and B to move them any higher in the priority list.
The same argument applies to A − B except in two cases. This is because in these two cases the subtraction is actually a multiplication by a negative, which is not at the bottom of the priority list! Here is the rule:
(A) − (B) simplifies to A − B except in these two cases: Exception # 1: If B is a negative monomial then the subtraction of a negative must be replaced by an addition. Exception # 2: If B is a multinomial then the − sign of the subtraction must be distributed over each term of the multinomial. The result, as explained below, is that each term of B has its sign reversed when the brackets are dropped. |
Examples:
- (x y) + (x z 2 ) simplifies to
x y + x z 2
- (x y) + (w + x z 2 ) simplifies to
x y + w + x z 2
- (x y) − (x z 2 ) simplifies to
x y − x z 2
- (x y) − (− x z 2 ) simplifies to
x y + x z 2
(this is exception # 1; subtracting a negative is adding)
- (x y) − (a + b) simplifies to
x y − a − b
(this is exception 2; you must distribute the − sign)
- (x y) − (− x z 2 + 5) simplifies to
x y + x z 2 − 5
(this is exception # 2; you must distribute the − sign)
Explanation of Exception 2: Why does distributing a − sign cause each term in the brackets to have its sign reversed? For example, why does a − (b − c) simplify to a − b + c ? Here is the sequence of steps with an explanation of each step:
a − (b − c) ← start with this a − (b + (− c) ) change subtraction into addition of a negative a + (− 1) · (b + (− c) ) change the other subtraction into multiplication by − 1 a + (− 1) · b + (− 1) · (− c) use the distributive law to distribute the − 1 a − b + (− 1) · (− c) change multiplication by − 1 back to subtraction a − b + c a negative times a negative gives a positive
Combining like terms
Recall that like terms are terms in an expression that differ only in their coefficients; they have identical variable factors. Like terms can be added or subtracted by adding or subtracting their coefficients (essentially by factoring with the distributive law). |
Here are some examples. The first two examples are done in detail. Assume that x and y are variables. In the last example assume that a and b are constants. The like terms are shown in red.
Example: Simplify the expression
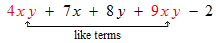
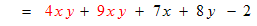
use the commutative law to sort the terms 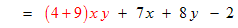
use the distributive law to combine (factor) the two like terms 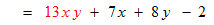
simplify
Example: Simplify the expression
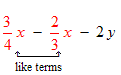
Example: Simplify the expression
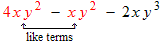
Example: Simplify the expression
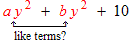
Note: In this last example the two terms in red were considered to be like terms because we were told that a and b are constants. If instead a and b were variables then the two terms in red would not be like terms and would NOT be combined.
3.3 - Integer Exponents
In the following two sections, section 3.4 on multiplying expressions and section 3.5 on dividing expressions, it will be necessary to understand exponentials with integer exponents. For that reason we study integer exponents now. Later, when we study logarithms, we will need to understand exponents that are not integers. Click here to go to that topic.When the exponential notation, b n, is first introduced to students, it is defined to mean repeated multiplication:
where there are a total of n factors of b, and n can be any natural number, 1, 2, 3, …. The number b is called the base, n is called the exponent, and we say that we are “raising b to the n th power” (except when n is 2 we say that we are “squaring b” and when n is 3 we say that we are “cubing b”). Here are some examples showing exponentials and what they mean:
- 2 4 = 2 · 2 · 2 · 2 = 16
- (−2) 4 = (−2) · (−2) · (−2) · (−2) = 16
- − 2 4 = − 2 · 2 · 2 · 2 = −16
Exponentials with the same base b have these three properties:
Multiplication property 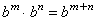
Division property 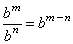
Exponentiation property 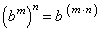
The following three examples show why these properties are true for any positive integer exponents:
Let’s assume that these properties can be generalized to exponents that are not necessarily positive integers. Then we can also give meaning to zero and negative integer exponents. Here’s how:
The meaning of b 0 : Let n = m in the division property. This gives:
On the other hand the numerator and denominator are equal:
| Putting this together we find that b 0 = 1. In other words any base raised to the 0th power equals 1. |
The meaning of b − n : Let m = 0 in the division property. This gives:
On the other hand the numerator equals 1:
Putting this together we find that:
In other words any base raised to a negative power is the reciprocal of the same base raised to the corresponding positive power.
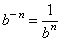
Notes:
- An especially useful case is when the exponent is −1.
The result is the reciprocal. Here are some examples:
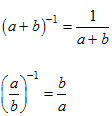
Here in detail is how the −1 exponent produced the reciprocal in the last example: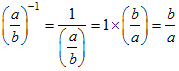
- We can’t raise zero to a negative power because then we get division by zero.
Exponentials whose bases are products or quotients
An exponential whose base is a product can be expanded like this:Here is the proof:

Similarly, an exponential whose base is a quotient can be expanded like this:
Here is the proof:
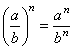
Here is an example of an expansion that combines several of these concepts:
3.4 - Multiplication of Expressions
Before studying this topic you may wish to review the multiplication of numbers and the properties of exponents.Suppose that A and B are any two expressions. Multiplying A and B means setting up the product as (A) · (B), and then actually carrying out the multiplication.
The reason that we put brackets around A and B is that they are expressions, not just numbers, and the multiplication is supposed to apply to whatever A and B may contain. (We want the multiplication to be at the end in the order of operations.)
How the multiplication is actually carried out depends on whether A and B are monomials or multinomials:
- Case I: A and B are both monomials
- Case II: One of A and B is a monomial
and the other is a multinomial
- Case III: A and B are both multinomials
Case I: multiplying two monomials
In this case we are multiplying monomials, and you may recall that monomials consist of factors that are already multiplied together. The associative law says that it doesn't matter in what order we carry out all the multiplications. Thus the brackets around the monomials can simply be dropped. (However we must pay attention to the rules for signs and move any minus sign to the front.)
Once the brackets have been removed then we simplify as much as possible. The commutative law is used to move the coefficients to the front and to rearrange the literals (letters) in alphabetical order. Then coefficients are multiplied, and like factors are combined using the properties of exponents.
Example: Multiply and simplify
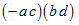
Example: Multiply and simplify
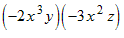
Example: Multiply and simplify
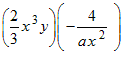
Case II: Multiplying a monomial by a multinomial
In this case the distributive law is used to remove the brackets. The monomial is distributed over each term of the multinomial. Then each resulting term is simplified as in Case I above.
Note that the Algebra Coach does not distribute a monomial over a multinomial when you click the Simplify button. You must use the Expand button to do that. The reason is that the factored form of an expression is usually considered to be simpler than the expanded form.
Example: Multiply and simplify
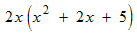
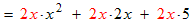
Use the distributive law to remove the brackets. 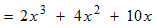
Simplify each term using the properties of exponents.
Example: Multiply and simplify
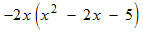
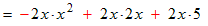
Distributing a negative monomial causes the signs in the multinomial (+ − −) to reverse (to become − + +). 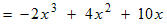
Simplify each term using the properties of exponents.
Case III: Multiplying two multinomials
In this case the distributive law is used to remove the brackets. Each term of the first multinomial is distributed over each term of the second multinomial. Then each resulting term is simplified as in Case I above. Finally, any like terms are combined.
Note that, as in case II, the Algebra Coach does not distribute a multinomial over a multinomial when you click the Simplify button. You must click the Expand button (several times) to do that. The reason is that the factored form of an expression is usually considered to be simpler than the expanded form.
Example: Multiply and simplify
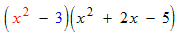

It is a good idea to show this “baby step” expansion where the second multinomial is kept together. 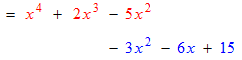
Expand twice more and line up the like terms. 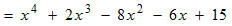
Combine the like terms.
Example: Multiply and simplify
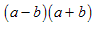
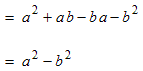
Expand using the foil method.
After canceling like terms, the result is a so-called difference of squares.
Example: Multiply and simplify
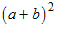
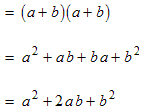
Write the square as the multinomial multiplied by itself.
Expand using the foil method.
Simplify. Compare this with the previous example. Here the like terms add instead of cancel.
3.5 - Division of Expressions
Before studying this topic you may wish to review common fractions and the division of numbers.Suppose that A and B are any two expressions. Dividing A by B means setting up the quotient as
(This quotient is called an algebraic fraction.) Then you actually carry out the division.
Note that in the first form,
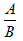 , (which is the preferred form),
no brackets are shown but they are implied.
The reason that we put brackets around A and B is
that they are expressions, not just numbers, and
the division is supposed to apply to whatever A and B may contain.
(We want the division to be at the end in the
order of operations.)
, (which is the preferred form),
no brackets are shown but they are implied.
The reason that we put brackets around A and B is
that they are expressions, not just numbers, and
the division is supposed to apply to whatever A and B may contain.
(We want the division to be at the end in the
order of operations.)
How the division is actually carried out and what the result is, depends on whether A and B are monomials, multinomials or polynomials:
- Case I: Numerator A and
denominator B are both monomials. We merely reduce the algebraic fraction
to lowest terms. The result of the division is a monomial.
- Case II: Numerator A
is a multinomial and denominator B is a monomial.
We place each term of the numerator over the denominator.
The result of the division is a multinomial.
- Case III: Numerator A and denominator B are both polynomials and the degree of A is higher than the degree of B. This is called an improper rational algebraic fraction. We divide the denominator into the numerator using long division (or synthetic division). The result of the division is a polynomial with possibly a proper rational algebraic fraction remainder.
Case I: Dividing a monomial by a monomial
In this case carrying out the division means just simplifying or reducing the resulting algebraic fraction to lowest terms. Specifically:
- Get the sign using the rules for signs.
- Reduce the coefficient to lowest terms.
- Cancel identical factors that appear in both the numerator and denominator.
- Combine exponentials having the same base using the division property of exponentials.
Example: Divide A = 6 b d by B = −9 a c

Reduce the coefficient 6/9 to lowest terms.
Notice that the − sign is put either in front of the result or in front of the numerator; never in front of the denominator.
Example: Divide A = −2 x 3 y by B = −8 x −2 z
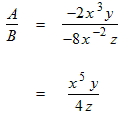
The two − signs are replaced by a + sign which we don’t have to display. The coefficient reduces to (positive) ¼. The numerator contains other factors so the 1 in the numerator can be omitted.
The factors with base x are like factors. They are combined using the properties of exponents.
Example: Divide A = −2 x 3 by B = 6 x 3 z

The coefficient reduces to −1/3. The identical factors of x 3 in the numerator and denominator cancel. The numerator contains no other factors so this time the 1 must remain.
Again the − sign is put in front.
Example: Divide B = 6 x 3 z by A = −2 x

After carrying out all the simplifications, the denominator equals 1, so we don’t have to display it. Thus the result is an ordinary expression, not an algebraic fraction.
Case II: Dividing a multinomial by a monomial
In this case each term of the multinomial is divided by the monomial like this:
and then each of the resulting terms is simplified as in Case I above.
This method is actually a consequence of replacing a division by a multiplication by a reciprocal and then using the distributive law to distribute the reciprocal onto each term of the multinomial, like this:
Note that the Algebra Coach does not divide a multinomial by a monomial when you click the Simplify button. You must use the Distribute button to do that. The reason is that the single fraction form of the expression is considered to be simpler than the multiple fraction form.
Example: Divide A = −2 x 4 z 2 − 3 x z by B = 6 x 3 z
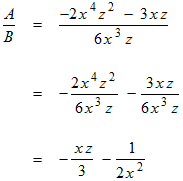
Divide each term of the multinomial by the monomial.
Simplify each term using the division property of exponents.
Example: Divide A = x 2 − 2 x − 5 by B = −2 x
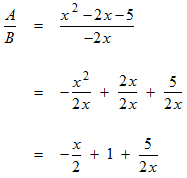
Divide each term of the multinomial by the monomial. Notice how the signs are reversed (just like when distributing a negative).
Simplify each term using the division property of exponents.
Warning: A common error is to try to simplify a monomial divided by a multinomial. However there is no simplification possible for this. |
Case III: Dividing a polynomial by a polynomial
An algebraic fraction whose numerator and denominator are both polynomials in the same variable is called a rational algebraic fraction. If the degree of the numerator polynomial is higher than the degree of the denominator polynomial then it is called an improper rational algebraic fraction. Just like long division can be used to convert an improper fraction to a mixed fraction (click here to review that topic), so long division can be used to convert an improper rational algebraic fraction into a polynomial plus a proper rational algebraic fraction (the analog of a mixed fraction).
Example: Divide 2 x 2 + 2 x − 3 by x − 2.
Carry out the following steps:
- Set up the algebraic fraction
 in long division format, namely
in long division format, namely  .
.
- We will call x − 2 the divisor and
2 x 2 + 2 x − 3 the dividend.
Divide the first term of the dividend, namely 2 x 2, by the first term of
the divisor, namely x. The result, 2 x, is written above the
 symbol, in line with the other x’s.
It will be the first term of the quotient. Multiply the divisor by the first
term of the quotient and write the result below the dividend and subtract it from the dividend,
like this:
symbol, in line with the other x’s.
It will be the first term of the quotient. Multiply the divisor by the first
term of the quotient and write the result below the dividend and subtract it from the dividend,
like this:
This step has shown that
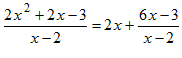 .
.
- We are not done yet. We repeat the previous step.
The divisor is again x − 2 but the remainder
from the previous step, namely 6 x − 3, becomes the new dividend.
Divide the first term of the dividend, namely 6 x, by the first term of
the divisor, namely x. The result, 6, is written above the
 symbol, in line with the other constants.
It will be the second term of the quotient. Multiply the divisor by the second
term of the quotient and write the result below the dividend and subtract it from the dividend,
like this:
symbol, in line with the other constants.
It will be the second term of the quotient. Multiply the divisor by the second
term of the quotient and write the result below the dividend and subtract it from the dividend,
like this:
This step has shown that: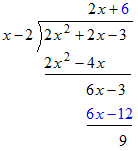

- Since the remainder, 9, is of lower degree than the divisor, x − 2, this is our final “mixed fraction” result.
Notes:
- Click here to compare this long division with that
of an improper fraction.
- When setting up the long division format the divisor and dividend must both be written in descending powers of the variable. Also if terms of either are missing they must be included with zero coefficients. For example if the dividend is 2 x − 3 x 3 then it must be rewritten as −3 x 3 + 0 x 2 + 2 x + 0.
3.6 - The Binomial and Multinomial Theorems
We have previously learned that a binomial is an expression that contains 2 terms and a multinomial is any expression that contains more than 1 term (so a binomial is actually a special case of a multinomial). We have also previously seen how a binomial squared can be expanded using the distributive law. For exampleIf we want to cube a binomial or raise it to an even higher power then we could do this by repeatedly applying the distributive law to lower powers. For example
But for very high powers this procedure is very laborious. The binomial theorem provides a shortcut. Similarly, the multinomial theorem provides a shortcut to expanding a multinomial raised to any positive integer power.
The Binomial Theorem
Take a look at these expansions of a binomial raised to power n, with n = 0, 1, 2, 3, 4 and 5.Let’s look for patterns in these expansions. Notice the following:
- In each expansion there are n + 1 terms.
(For example the bottom (n = 5) expansion has 6 terms.)
- The powers of x start at n and decrease by 1 in each term until they reach 0.
- The powers of y start at 0 and increase by 1 until they reach n.
- The coefficients in each expansion add up to 2n.
(For example in the bottom (n = 5) expansion the coefficients
1, 5, 10, 10, 5 and 1 add up to 25 = 32.)
- The coefficients are exactly the numbers that appear in
Pascal’s Triangle, shown here:
What is Pascal’s Triangle? It is an infinitely tall triangle of numbers that can be constructed as follows:
- The first number and the last number in each row is a 1.
- Every number in the interior of the triangle is the sum of the two numbers
above left and above right, like this:

- Pascal’s Triangle above is animated to show how each row is generated from the row above.
- Each number in Pascal’s triangle can also be generated using the so-called
combination function as shown here:
Pascal’s triangle is really just a listing of all the possible values of the combination function. The combination function is defined as
where n! or “n factorial” is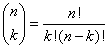
The combination function gives the number of distinct groups of k objects that can be chosen from n distinct objects when the order in which they are chosen doesn’t matter.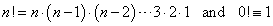
Here are some examples of calculations that use the combination function:
Example: From 4 people, how many distinct groups of 2 people be chosen to work on some project?
Solution: The answer is
If the persons are called A, B, C and D then the distinct groups are AB, AC, AD, BC, BD and CD.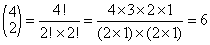
Example: In the expansion of (a+b)4 what is the coefficient of the term a3b?
Solution: The answer is 4. The reason is that the term a3b comes from multiplying a b from inside 1 of the brackets and a’s from inside the remaining 3 brackets. There are
ways of choosing which bracket the b should come from. The blue arrows show one of these ways: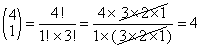

Putting all of this together gives the binomial theorem, which states that a power of a binomial can be expanded like this:
Using summation notation the binomial theorem can also be written like this: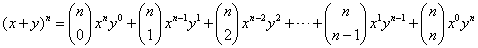
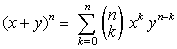
- The first number and the last number in each row is a 1.
The Multinomial Theorem
The multinomial theorem extends the binomial theorem. It describes the result of expanding a power of a multinomial. We will show how it works for a trinomial. Multinomials with 4 or more terms are handled similarly.Consider (a + b + c)4. The brute force way of expanding this is to write it as
(a + b + c) (a + b + c) (a + b + c) (a + b + c),then apply the distributive law, and then simplify by collecting like terms. After distributing, but before collecting like terms, there are 81 terms. (This is because every term in the first brackets has to be multiplied by every term in the second brackets, giving 9 terms. Each of these has to be multiplied by every term in the third brackets, giving 27 terms. Finally each of these has to be multiplied by every term in the fourth brackets, giving 81 terms.) Many of the terms look different before simplifying, but are identical after simplifying. For example the four terms abbb, babb, bbab and bbba (where the a comes from either the first, second, third or fourth brackets) can be simplified and collected to give 4ab3. Thus to understand the various coefficients in the final result shown below we need to consider what distinct terms can occur and how many ways there are of getting each of them:
Notice the following:
- There are 15 distinct terms.
- Each term is of degree 4.
- The coefficients add up to 34 = 81 (As mentioned above this is the
number of terms before collecting like terms.)
- Start with three nested summations:
The problem is that this triple summation produces 5·5·5=125 terms of various degrees ranging from a0b0c0 to a4b4c4.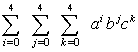
- Introduce a filter factor that equals 1 for the wanted terms
(those of degree 4) and 0 for the unwanted terms.
This is the Kronecker delta function,
denoted δi, j and defined as:
Now change the summation to read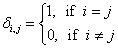
It contains only the 15 wanted terms of degree 4. The only remaining problem is that every coefficient equals 1.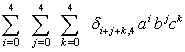
- Construct the correct coefficient. This is the so-called multinomial coefficient:
This multinomial coefficient gives the number of ways of depositing 4 distinct objects into 3 distinct groups, with i objects in the first group, j objects in the second group and k objects in the third group, when the order in which they are deposited doesn’t matter.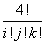
For example the coefficient of the a1b1c2 term uses i = 1, j = 1 and k = 2 and equals
With this coefficient the expansion reads
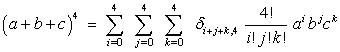
We can generalize this to give us the nth power of a trinomial. (Just change all the 4’s to n’s.)
This is the multinomial theorem for 3 terms. It easily generalizes to any number of terms. For example the multinomial theorem for 4 terms reads:
3.7 - Expression Trees
What is an expression tree?
A tree is a data structure that is useful for displaying data that is organized in a hierarchy. The actual data items are stored in locations called nodes and the relationships between the data items are represented by dotted lines called branches. One example is the Folders tree in Windows Explorer. Folders within other folders are displayed further to the right in the tree. Another example is the Table of Contents in the frame just to the left of what you are presently reading. Subtopics within other topics are displayed further to the right (indented) in the tree.A mathematical expression is also a hierarchy because of the order of mathematical operations, so it can also be displayed in a tree. For example the expression:
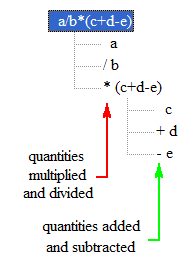
a/b*(c+d-e),which is typeset as:
is represented by the tree shown to the right.
The entire expression, a/b*(c+d-e), is contained in the root node of the tree. It is shown in blue.
This expression contains 3 “factors”, a, b and (c+d-3), that are either multiplied or divided together. Therefore 3 branches come out of this node and each of the factors goes into a node at the end of one of these branches. The red arrow points to these child nodes. (These nodes also contain a * or / symbol to indicate whether this factor is in the numerator or denominator.)
The expression in the third child node, (c+d-e), contains 3 terms, c, d, and e, that are either added or subtracted together. Therefore 3 branches come out of this node and each of the terms goes into a node at the end of one of these branches. The green arrow points to them. (These nodes also contain a + or - symbol to indicate whether this term is added or subtracted.)
This process of breaking the expression into ever smaller parts, with the tree growing from left to right, continues until every branch ends with a node containing either a number or a variable that represents a number.
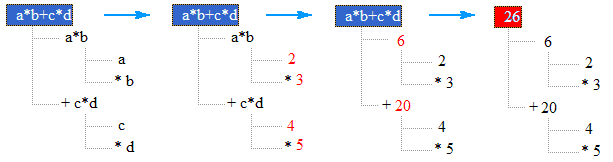
When an expression is evaluated, the evaluations travel back through the nodes from right to left. Every child node must have a value before its parent node can be evaluated. Here is an example showing how the expression a b + c d is evaluated with a = 2, b = 3, c = 4, d = 5. Follow the sequence of pictures and notice how the numbers shown in red appear.
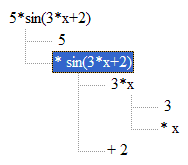 Functions are represented as shown in this example:
Functions are represented as shown in this example:
5 sin (3 x + 2).The node containing the function (shown in blue) is the root of a brand new tree that holds the argument of the function. Before the function can be evaluated this tree must be evaluated.
 Exponentials are represented as shown in this example of the expression:
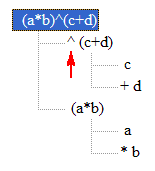
Exponentials are represented as shown in this example of the expression:
The node containing the exponential (shown in blue) is the root of two new trees, one that holds the exponent (indicated by the caret symbol, ^, and pointed to by the red arrow) and one that holds the base. Before the exponential can be evaluated both of these trees must be evaluated.
What can an expression tree show you?
An expression tree is useful for:- Understanding the order of operations.
Operations that must be done sooner are further to the right in the tree.
- Counting the number of terms or factors in an expression. Each term or factor is a child node. For example the expression (a+b)/c+2*d contains two terms. Hint: You can collapse or hide a node's children by clicking on the node and then pressing the left arrow key. You an make the children reappear by pressing the right arrow key. This picture shows the collapsed view on the left and the expanded view on the right: