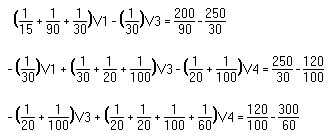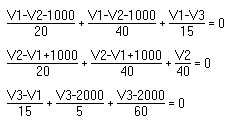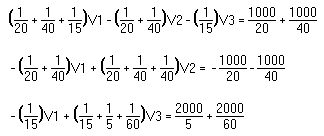Analysing Electric Networks

Analysing an electric circuit means to find the voltage and current at every point in the circuit. A basic electric circuit is one where this can be done using only the formulas for resistors in series and parallel. But there are many circuits such as the one shown to the right where this cannot be done. Then we must use loop analysis or nodal analysis to write down a system of equations describing the circuit. Then we can use Gaussian elimination to solve this system of equations.
Loop analysis finds the currents directly and nodal analysis find the voltages directly. Which method is simpler depends on the given circuit. Knowing the branch currents, the nodal voltages can easily be calculated, and knowing the nodal voltages, the branch currents can easily be calculated.
Basic Electric Circuits
Here is an electric circuit diagram: Notice these symbols:
Notice these symbols:
- The
 symbol for a voltage source
(this could be for example a battery). Voltage sources generate a force or "pressure"
which causes electric currents to flow in the circuit. The voltage source shown is rated
at 10 volts (abbreviation V). This means that the voltage or "pressure" is 10 volts higher
at the plus (+) side of the battery than at the minus (−) side of the battery.
As a result, electric charges are given a force in the upward direction
(from the − side to the + side).
symbol for a voltage source
(this could be for example a battery). Voltage sources generate a force or "pressure"
which causes electric currents to flow in the circuit. The voltage source shown is rated
at 10 volts (abbreviation V). This means that the voltage or "pressure" is 10 volts higher
at the plus (+) side of the battery than at the minus (−) side of the battery.
As a result, electric charges are given a force in the upward direction
(from the − side to the + side).
- The
 symbol for a resistor.
Resistors are devices that impede the flow of electric current. The resistor at the lower
right has a resistance of 55 ohms (abbrev
symbol for a resistor.
Resistors are devices that impede the flow of electric current. The resistor at the lower
right has a resistance of 55 ohms (abbrev  ).
).
- The
 symbol for a wire. A wire is assumed
to have no resistance.
symbol for a wire. A wire is assumed
to have no resistance.
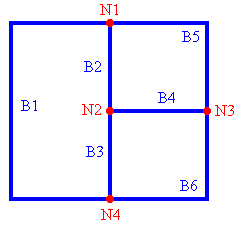
Principal Nodes or Junctions and Branches
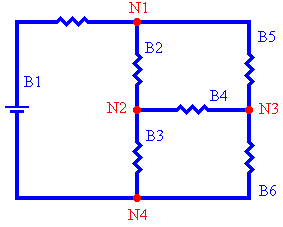 In this diagram we define:
In this diagram we define:
- principal nodes or junctions - These are points where 3 or more wires meet.
This circuit contains 4 of them, denoted N1, ..., N4. Notice the
 symbol for a principal node.
symbol for a principal node.
- branches - A branch is any path in the circuit that has a node at each end and
contains at least one voltage source or resistor but contains no other nodes. This circuit
contains 6 branches, denoted B1, ..., B6.
(Note: If branch B4 did not contain a resistor then it could be deleted and nodes N2 and N3 could be considered one and the same node.)
Electric Current
Electric charge flowing in a branch in a circuit is analogous to water flowing in a pipe. The rate of flow of charge is called the current. It is measured in coulombs/second or amperes (abbreviation A) just as the flow rate of water is measured in liters/second.Water is incompressible, which means that if 1 liter of water enters one end of a length of pipe then 1 liter must exit from the other end. The situation is the same with electric current. If the current is 1A at a certain point in a branch then it is 1A everywhere else in that branch.
Kirchhoff's Current Law
An immediate consequence of this is Kirchhoff's Current Law. Kirchhoff's current law states that the sum of the currents flowing into a node equals the sum of the currents flowing out of the node. Here is an example: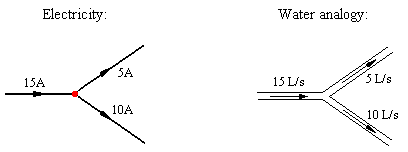
This diagram also shows how we draw an arrow on the branch to indicate the current flowing in the branch.
Electric Voltage
Electric current is the flow of electric charges. Electric voltage is the force that causes this flow. Just as a pump pushes a "plug" of water through a pipe by creating a pressure difference between its ends, so a battery pushes charge through a resistor by creating a voltage difference between the two ends of the resistor. The picture shows the analogy:
This diagram also shows how we draw an arrow beside a resistor or any other device to indicate a voltage difference between the two ends of that device. The arrow head is drawn pointing to the higher voltage end.
Ohm's Law
We have just seen that a voltage difference between the two ends of a resistor causes a current to flow through the resistor. For many substances the voltage and current are proportional. This is expressed by the formula:V = I R,This equation is called Ohm's law and any device that obeys it is called a resistor.
V is the difference in voltage between the two ends of the resistor measured in volts, I is the current through the resistor measured in amperes, and the proportionality constant R is the resistance of the resistor measured in ohms. Given any two of these quantities, Ohm's law can be used to find the third.
Kirchhoff's Voltage Law
Just as the water pressure drops in a garden hose the farther one moves away from the tap, so the voltage changes as one moves around a circuit away from a voltage source. Kirchhoff's Voltage Law states that:Around any closed path in an electric circuit, the sum of the voltage drops through the resistors equals the sum of the voltage rises through the voltage sources.A closed path is a path through a circuit that ends where it starts.
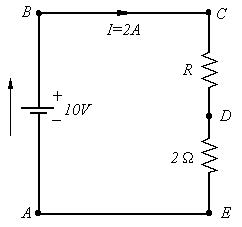 Problem: Resistors in Series. Use Kirchhoff's voltage law and Ohm's law to find the value
of the unknown resistor R if it is known that a 2 ampere current flows in the circuit.
Problem: Resistors in Series. Use Kirchhoff's voltage law and Ohm's law to find the value
of the unknown resistor R if it is known that a 2 ampere current flows in the circuit.Solution: Let's follow the current as it flows clockwise around the circuit. If we start at A and assume the voltage there is 0 then at B the voltage must be 10 volts because the battery behaves like a pump that creates a higher pressure at the + side than the − side. At C the voltage is still 10 volts but it drops going to D through resistor R, and drops again going to E through the 2 ohm resistor. In fact it must return to 0 volts since A and E are at the same voltage (voltage does not change along an ideal wire that has no resistance).
Using Ohm's Law in the form V = I R we find that the I R (voltage) drop across the 2
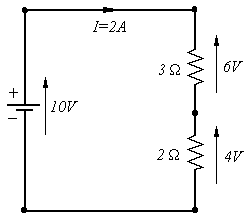
The results are shown to the right. Notice the directions of the voltage arrows across each of the devices.
Also notice that the voltage drops across the two resistors are proportional to their resistances.
This is called the Voltage Divider Rule. This rule is useful in many situations.
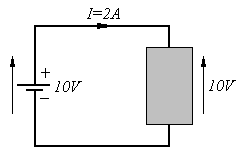
Suppose that we replaced the above circuit by the one shown to the right and didn't know what was inside the "black box" but did know that the current flowing into the black box was 2 A and that the voltage across it was 10 V. Then Ohm's law, R = V / I, would tell us that the black box had a resistance of 5
This is true in general: two resistors R1 and R2 in series may be replaced by a single equivalent resistor Req whose resistance is the sum of the two resistances:
Req = R1 + R2.
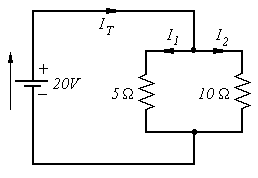 Problem: Resistors in Parallel. Find the value of the total current IT
flowing into the parallel circuit.
Problem: Resistors in Parallel. Find the value of the total current IT
flowing into the parallel circuit.Solution: Since there is no voltage drop along a wire, 20 V appears across each resistor. Using Ohm's Law in the form I = V / R we find:
I1 = 20 V / 5
and:
I2 = 20 V / 10
and by Kirchhoff ' s Current Law IT = 4 A + 2 A = 6 A.
Notes:
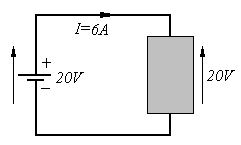 Suppose that we replaced the above circuit by the one shown to the right and didn't know what
was inside the "black box" but did know that the current flowing into the black box was
IT = 6 A and that the voltage across it was 20 V. Let's call its resistance
Req. Ohm's law in the form I=V/R says that:
Suppose that we replaced the above circuit by the one shown to the right and didn't know what
was inside the "black box" but did know that the current flowing into the black box was
IT = 6 A and that the voltage across it was 20 V. Let's call its resistance
Req. Ohm's law in the form I=V/R says that:But when we could see inside we had:
Comparing these two expressions for IT gives (after cancelling out the common factor of 20 V):
This formula is true in general: two resistors R1 and R2 in parallel may be replaced by a single equivalent resistor Req given by the formula:
Loop Analysis of Electric Circuits
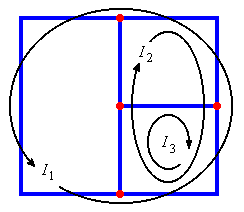
In this method, we set up and solve a system of equations in which the unknowns are loop currents. The currents in the various branches of the circuit are then easily determined from the loop currents. (Click here for a tutorial on loop currents vs. branch currents.)
The steps in the loop current method are:
- Count the number of loop currents required. Call this number m.
- Choose m independent loop currents, call them I1, I2, . . . , Im and draw them on the circuit diagram.
- Write down Kirchhoff's Voltage Law for each loop. The result, after simplification, is a system of n linear equations in the n unknown loop currents in this form:
where R11, R12, . . . , Rmm and V1, V2, . . . , Vm are constants.
Alternatively, the system of equations can be gotten (already in simplified form) by using the inspection method.
- Solve the system of equations for the m loop currents I1, I2, . . . , Im using Gaussian elimination or some other method.
- Reconstruct the branch currents from the loop currents as described in the tutorial above.

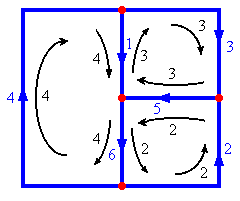
Example 1: Find the current flowing in each branch of this circuit.
Solution:
- The number of loop currents required is 3.

- We will choose the loop currents shown to the right. In fact these loop currents are
mesh currents.
- Write down Kirchoff's Voltage Law for each loop. The result is the following system of equations:
Collecting terms this becomes: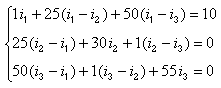
This form for the system of equations could have been gotten immediately by using the inspection method.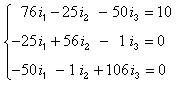
- Solving the system of equations using Gaussian elimination or some other method gives the
following currents, all measured in amperes:
I1=0.245, I2=0.111 and I3=0.117
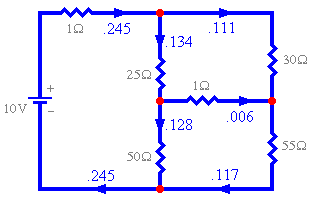
- Reconstructing the branch currents from the loop currents gives the results shown in
the picture to the right.
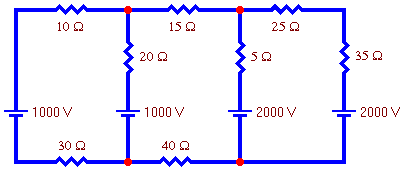
Example 2: Find the current flowing in each branch of this circuit.
Solution:
- The number of loop currents required is 3.
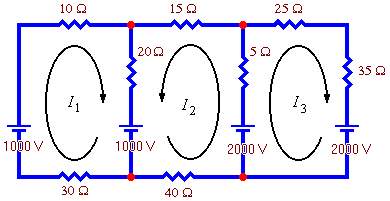
- This time we will choose the loop currents shown to the right.
- Write down Kirchoff's Voltage Law for each loop. The result is the following system of equations:
Collecting terms this becomes: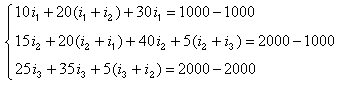
This form for the system of equations could have been gotten immediately by using the inspection method.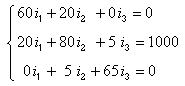
- Solving the system of equations using Gaussian elimination or some other method gives the
following currents, all measured in amperes:
I1 = −4.57, I2 = 13.7 and I3 = −1.05
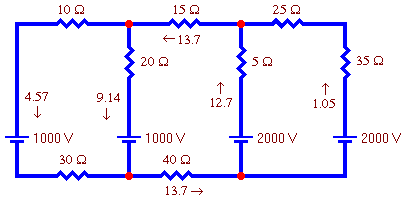
- Reconstructing the branch currents from the loop currents gives the results shown in the
picture to the right.
Nodal Analysis of Electric Circuits
In this method, we set up and solve a system of equations in which the unknowns are the voltages at the principal nodes of the circuit. From these nodal voltages the currents in the various branches of the circuit are easily determined.The steps in the nodal analysis method are:
- Count the number of principal nodes or junctions in the circuit. Call this number n.
(A principal node or junction is a point where 3 or more branches join. We will indicate
them in a circuit diagram with a red dot. Note that if a branch contains no voltage sources or
loads then that entire branch can be considered to be one node.)
- Number the nodes N1, N2, . . . , Nn and draw
them on the circuit diagram. Call the voltages at these nodes V1, V2,
. . . , Vn, respectively.
- Choose one of the nodes to be the reference node or ground and assign it a voltage of zero.
- For each node except the reference node write down Kirchoff's Current Law in the form "the
algebraic sum of the currents flowing out of a node equals zero". (By algebraic sum we mean
that a current flowing into a node is to be considered a negative current flowing out of the node.)
 For example, for the node to the right KCL yields the equation:
For example, for the node to the right KCL yields the equation:
Ia + Ib + Ic = 0
Express the current in each branch in terms of the nodal voltages at each end of the branch using Ohm's Law (I = V / R). Here are some examples:

The current downward out of node 1 depends on the voltage difference V1 − V3 and the resistance in the branch.

In this case the voltage difference across the resistance is V1 − V2 minus the voltage across the voltage source. Thus the downward current is as shown.

In this case the voltage difference across the resistance must be 100 volts greater than the difference V1 − V2. Thus the downward current is as shown.
The result, after simplification, is a system of m linear equations in the m unknown nodal voltages (where m is one less than the number of nodes; m = n − 1). The equations are of this form:
where G11, G12, . . . , Gmm and I1, I2, . . . , Im are constants.
Alternatively, the system of equations can be gotten (already in simplified form) by using the inspection method.
- Solve the system of equations for the m node voltages V1,
V2, . . . , Vm using Gaussian elimination
or some other method.

Example 1: Use nodal analysis to find the voltage at each node of this circuit.
Solution:
- Note that the "pair of nodes" at the bottom is actually 1 extended node. Thus the number of
nodes is 3.

- We will number the nodes as shown to the right.
- We will choose node 2 as the reference node and assign it a voltage of zero.
- Write down Kirchoff's Current Law for each node. Call V1 the voltage at node 1,
V3 the voltage at node 3, and remember that V2 = 0.
The result is the following system of equations:
The first equation results from KCL applied at node 1 and the second equation results from KCL applied at node 3. Collecting terms this becomes:
This form for the system of equations could have been gotten immediately by using the inspection method.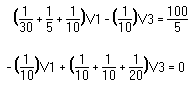
- Solving the system of equations using Gaussian elimination or some other method gives the
following voltages:
V1=68.2 volts and V3=27.3 volts
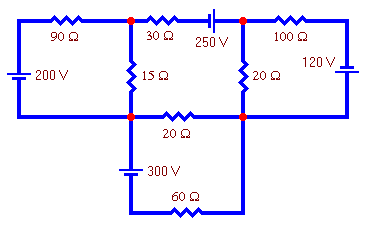
Example 2: Use nodal analysis to find the voltage at each node of this circuit.
Solution: Click here for solution.

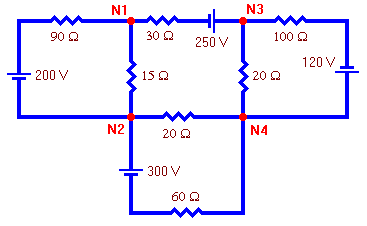
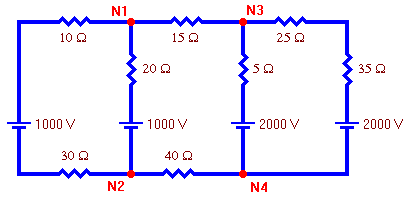
Example 3: Use nodal analysis to find the voltage at each node of this circuit.
Solution: Click here for solution.
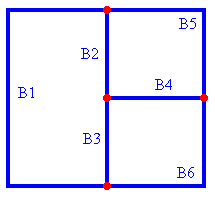
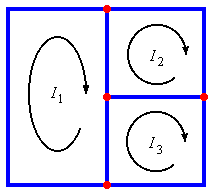
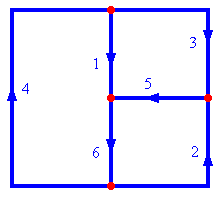 Each branch current is given by the algebraic sum of all the loop currents present in that branch.
(By algebraic sum we mean that the sign and direction of loop currents must be taken into account
in the sum.)
Each branch current is given by the algebraic sum of all the loop currents present in that branch.
(By algebraic sum we mean that the sign and direction of loop currents must be taken into account
in the sum.)