The Travelling Salesman Problem

The Travelling Salesman Problem (TSP) is one of the most intensively studied problems in computer science. If it was introduced today it might be called the courier problem, since couriers delivering packages are faced with the same issues.
Suppose that you are a salesperson and you must visit 20 cities spread across North America. You must visit each city once (and only once) and return home. The problem is this: In what order should you visit them to minimize the total distance that you have to travel?
If the cities lie in a ring then the answer is probably obvious – go around the ring. But often the cities are located such that there is no obvious answer.
Then there is only one way to find the shortest path and that is to write down every possible ordering of the cities, calculate the distance for each of those orderings, and pick the shortest one.
Contents of this page
- Counting the Possible Orderings
- The Factorial Function
- Tree Diagram of the Possible Paths
- Nested Loops Code for the Possible Paths
- Recursion
- Recursive Code for the Possible Paths
- Recursive Code for the Travelling Salesman Problem
- Time Taken to Run the Code
Counting the Possible Orderings
Another word for ordering is permutation. How many orderings of the cities or permutations are there? They can be counted this way:
- For the first city to visit you have 20 choices.
- For the second city to visit you then have only 19 choices (because you don't visit the first city again).
- For the third city you have 18 choices,
- and so on . . .
- For the last city you have 1 choice
These numbers must be multiplied together to give the total number of orderings:
= 2,432,902,008,176,640,000 possible orderings
How big is this number? Well, my computer (which has an Intel Core I5 processor) can check about 40,000 orderings per second. At this rate it would take 2 million years to check them all! Thus even though we have a way to solve the Travelling Salesman Problem, we still can't do it.
The Factorial Function
The type of multiplication described above occurs so often in counting permutations that we give it a name – factorial.
Definition: the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n.
Thus the above multiplication is written as 20! and is spoken as "twenty factorial".
Look for the factorial function on your calculator. Here are more examples:- 2! = 2 × 1 = 2
- 5! = 5 × 4 × 3 × 2 × 1 = 120
- 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3628800
- 69! = 1.71x1098 (the biggest number my calculator can display)
The reason that the number n is a non-negative integer is that we use it for counting permutations or arrangements of whole objects. And since we could have zero objects (e.g. no cities to visit) we also define 0! It doesn't fit the pattern but it makes sense to define it to equal 1.
Tree Diagram of the Possible Paths
We saw above that it is easy to count the number of possible paths. Now we want to learn how to make a list of the paths.

This tree diagram shows that for 4 cities there are 24 possible paths. The cities are named "1", "2", "3" and "4". Slotn refers to the nth city visited. The top path is "1234" and the bottom path is "4321".
The picture to the right shows a tree diagram that describes the possible paths for visiting four cities. Paths are made by putting cities into slots. Slot1 is first city visited, Slot2 is the second city visited, etc. Suppose that the cities are named "1", "2", "3" and "4".
The top six paths (colored red) describe visiting city "1" first and then the other cities in various orders. Similarly, the bottom red part of the tree describes visiting city "4" first and then the other cities in various orders.
The numbers in the bottom red part of the tree show how a path is built up as city after city is added to the path.
The top path in this tree is "1234" and the bottom path is "4321".
Nested Loops Code for the Possible Paths
The rest of this blog is about writing Visual Basic (VB) code to solve the Travelling Salesman Problem (TSP) exactly for a small number of cities. In a future blog page we will describe how to solve it approximately for a large number of cities using a method called simulated annealing.
You can click here to go to a blog page that gives an introduction to VB programming in Excel. Also, you can save yourself some typing and click here to download an Excel spreadsheet containing all of the code.
Let's begin by writing code to list all the possible paths.
One way to do it is to use nested loops.
Here is a procedure that does it for 4 cities.
It displays a message box 4! or 24 times showing the possible paths.
To run the subroutine, copy it into an Excel module and enter the
command Call FourLoops in the
Immediate window.
Sub FourLoops() '1
Dim Slot1 As Integer, Slot2 As Integer, Slot3 As Integer, Slot4 As Integer '2
Dim Count As Integer, Path As String '3
For Slot1 = 1 To 4 'Slot1 is the 1st city visited '4
For Slot2 = 1 To 4 '5
If Not (Slot2 = Slot1) Then '6
For Slot3 = 1 To 4 '7
If Not (Slot3 = Slot1 Or Slot3 = Slot2) Then '8
For Slot4 = 1 To 4 'Slot4 is the 4th city visited '9
If Not (Slot4 = Slot1 Or Slot4 = Slot2 Or Slot4 = Slot3) Then '10
Path = CStr(Slot1) & CStr(Slot2) & CStr(Slot3) & CStr(Slot4) '11
Count = Count + 1 '12
Call MsgBox("Path # " & Count & " is " & Path) '13
End If '14
Next Slot4 '15
End If '16
Next Slot3 '17
End If '18
Next Slot2 '19
Next Slot1 '20
End Sub '21
Lines 4, 5, 7 and 9 contain the nested For loops. Lines 6, 8 and 10 contain If statements that ensure that the paths are valid. Lines 11 to 13 are the block of code that gets executed with every iteration.
Recursion
The problem with the above code is that if we want to list the possible paths for, say, 10 cities then we need to write a new procedure that uses 10 nested loops.
A more versatile way to make the list is with recursion. Recursion means "defining a problem in terms of itself". Here is a VB subroutine that calls itself recursively:
Sub Iterate(Iteration As Integer) '1
Iteration = Iteration + 1 '2
Call Iterate(Iteration) '3
End Sub '4
Line 3 does the recursion. Line 2 counts the number of times that Iterate calls itself. The program crashes after about 6000 recursions with the message "Out of stack space". Clearly, when using recursion there must be a way to stop after some desired number of iterations.
The classic example of recursion with a stopping criterion is the factorial function, which can be defined recursively like this:
The upper version of the definition contains the recursion and the lower version contains
the stopping criterion.
For example, 4!
= 4 × 3!
= 4 × 3 × 2!
= 4 × 3 × 2 × 1!
= 4 × 3 × 2 × 1
Here is the recursive VB code for the factorial function.
Public Function Factorial(N As Integer) As Double '1
If N > 1 Then '2
Factorial = N * Factorial(N - 1) '3
Else '4
Factorial = 1 '5
End If '6
End Function '7
To use the function type =Factorial(x) into any spreadsheet cell
(where x is any positive integer).
Recursive Code for the Possible Paths
We are now ready to write some code that uses recursion to list the possible
paths for 4 cities. Here it is. You can paste it into a module in Excel and run
it by entering the command Call PutCityInSlot(1) in the Immediate window.
Private Const Cities = 4 'Number of cities to visit. '1
Private Count As Integer 'Number of paths checked. On exit Count = Cities! '2
Private Path As String 'e.g. Path="132" means visit city 1, then 3, then 2. '3
Private Sub PutCityInSlot(Slot As Integer) '4
'Slot is a position in the Path. City is a city's number (name).
'e.g. Slot = 3 and City = 7 means that the third city visited is city 7.
Dim City As Integer '5
For City = 1 To Cities 'City runs through all cities. '6
If ValidPath(CStr(City), Slot) Then 'Check that this City is new. '7
Path = Left(Path, Slot - 1) & CStr(City) 'Add this City to the Path. '8
If Slot < Cities Then 'If still building up the Path '9
Call PutCityInSlot(Slot + 1) 'then iterate to get next city. '10
Else 'Otherwise '11
Count = Count + 1 'we have a complete Path. '12
Call MsgBox("Path # " & Count & " is " & Path) '13
End If '14
End If '15
Next City '16
End Sub '17
Private Function ValidPath(City As String, Slot As Integer) As Boolean '18
'Returns True if it is valid to put this City in this Slot
'(i.e. City hasn't already appeared before position Slot)
Dim I As Integer '19
For I = 1 To Slot - 1 '20
If Mid(Path, I, 1) = City Then Exit Function '21
Next I '22
ValidPath = True '23
End Function '24
Some notes on the code:
- Line 1 sets the number of cities to visit to a manageable 4. Making it bigger means that many more message boxes get displayed. (If required, you can "kill" the program by pressing Ctrl-Break on your keyboard.)
- Lines 2 and 3 make the two variables Count and Path global. This means that all recursions of subroutine PutCityInSlot are accessing the same two variables.
- Lines 4 to 17 are the main routine, called PutCityInSlot. Line 10 contains the recursion. Lines 12 and 13 are the block of code that gets executed with every recursion. If we compare routine PutCityInSlot to the nested loops procedure, FourLoops, above, we see that each recursion does the same job as one nested loop of FourLoops.
- Lines 18 to 24 are a utility function, called ValidPath. This function relaces all of the If statements in routine FourLoops.
Recursive Code for the Travelling Salesman Problem
We are now ready to write a program that uses recursion to solve the Travelling Salesman Problem. Take a look at this spreadsheet:

The range B3:D12 holds the names of the home city (0) and nine cities to visit (1 to 9) and their x and y coordinates. This is the input to the program. A scatter plot with markers shows the cities.
The program runs through all the possible paths (for 9 cities there are 362,880 of them) and finds the shortest one (in this example, the shortest path is "172349865"). It outputs this path to range B18:D28 and displays it in a scatter plot with markers and connecting lines.
The code is divided into two parts: the main part and the I/O
(input and output) part. The two parts can be copied into a module in Excel
and run by entering the command Call TSP_recursive in the Immediate window.
Private Const Cities = 9 'number of cities to visit. 1
Private Count As Long 'Number of paths checked. On exit = Cities! 2
Private Path As String 'e.g. Path="132" means visit city 1, then 3, then 2. 3
Private ShortPath As String, ShortDist As Single '4
'shortest path and its distance
Private Dist_Table(0 To Cities, 0 To Cities) As Single '5
'element I,J is the distance from city I to J
'--------------------------------------------------------------------------------------
Public Sub TSP_recursive() '6
'go from "home" city 0 to "away" cities 1, 2, 3 ..., Cities, and return to 0
Dim XCity(0 To Cities + 1) As Single, YCity(0 To Cities + 1) As Single '7
Dim TimeStart As Single, TimeFinish As Single '8
TimeStart = Timer '9
Count = 0 '10
ShortDist = 1E+30 '11
'Step 1. Input the city coordinates.
Call Input_City_Coordinates(3, 3, XCity, YCity) '12
'Step 2. Create the table of intercity distances.
Call Create_Dist_Table(XCity, YCity) '13
'Step 3. Run through all paths and find the shortest.
Call PutCityInSlot(1) '14
'Step 4. Output the shortest path to the spreadsheet.
Call Output_Path(XCity, YCity, ShortPath, 18, 2) '15
TimeFinish = Timer '16
MsgBox "Cities: " & Cities & ", Paths: " & Count & _
", Time: " & Format((TimeFinish - TimeStart) * 1000, "0") & "ms" '17
End Sub '18
'--------------------------------------------------------------------------------------
Private Sub PutCityInSlot(Slot As Integer) '19
'Slot is a position in the Path. City is a city's number (name).
'e.g. Slot = 3 and City = 7 means that the third city visited is city 7.
Dim City As Integer, Dist As Single '20
For City = 1 To Cities 'City runs through all cities. 21
If ValidPath(CStr(City), Slot) Then 'Check that this City is new. 22
Path = Left(Path, Slot - 1) & CStr(City) 'add this City to the Path 23
If Slot < Cities Then 'If still building up the Path 24
Call PutCityInSlot(Slot + 1) 'then iterate to get next city. 25
Else 'Otherwise, we have a complete Path. 26
Count = Count + 1 'Count it and 27
Dist = PathLength(Path) 'get its length. 28
If Dist < ShortDist Then 'Record the shortest path. '29
ShortDist = Dist '30
ShortPath = Path '31
End If '32
End If '33
End If '34
Next City '35
End Sub '36
'--------------------------------------------------------------------------------------
Private Function ValidPath(City As String, Slot As Integer) As Boolean '37
'Returns True if it is valid to put this City in this Slot
'(i.e. City hasn't already appeared before position Slot)
Dim I As Integer '38
For I = 1 To Slot - 1 '39
If Mid(Path, I, 1) = City Then Exit Function '40
Next I '41
ValidPath = True '42
End Function '43
Private Sub Input_City_Coordinates(Row, Col, XCity, YCity) '44
'Step 1. Read the City names (numbers) and coordinates from the spreadsheet.
'To make the loops easier, XCity(0) and XCity(Cities + 1) both refer to
'the home city; the rest refer to the away cities 1, 2, 3,..., Cities
Dim I As Integer '45
For I = 0 To Cities '46
XCity(I) = Cells(Row + I, Col) '47
YCity(I) = Cells(Row + I, Col + 1) '48
Next I '49
XCity(Cities + 1) = XCity(0): YCity(Cities + 1) = YCity(0) '50
End Sub '51
'--------------------------------------------------------------------------------------
Private Sub Create_Dist_Table(XCity, YCity) '52
'Step 2. Create the table of intercity distances.
Dim I As Integer, J As Integer '53
For I = 0 To Cities - 1 '54
For J = I + 1 To Cities '55
Dist_Table(I, J) = Sqr((XCity(I) - XCity(J)) ^ 2 + (YCity(I) - YCity(J)) ^ 2) '56
Dist_Table(J, I) = Dist_Table(I, J) '57
Next J '58
Next I '59
End Sub '60
'--------------------------------------------------------------------------------------
Private Sub Output_Path(XCity, YCity, Path, Row, Col) '61
'Step 4. Output the shortest path to the spreadsheet.
Dim I As Integer, Idx As Integer '62
For I = 0 To Cities + 1 '63
If I = 0 Or I = Cities + 1 Then Idx = 0 Else Idx = Mid(Path, I, 1) '64
Cells(Row + I, Col) = Idx '65
Cells(Row + I, Col + 1) = XCity(Idx) '66
Cells(Row + I, Col + 2) = YCity(Idx) '67
Next I '68
End Sub '69
'--------------------------------------------------------------------------------------
Private Function PathLength(Path As String) As Single '70
'This function returns the Length of a Path
Dim I As Integer, Idx1 As Integer, Idx2 As Integer '71
For I = 1 To Cities + 1 'loop over the legs '72
If I <> 1 Then '73
Idx1 = CInt(Mid(Path, I - 1, 1)) 'the 'from' city number '74
Else '75
Idx1 = 0 'first leg is from the home number 76 '60
End If '77
If I <> Cities + 1 Then '78
Idx2 = CInt(Mid(Path, I, 1)) 'the 'to' city number '79
Else '80
Idx2 = 0 'last leg is to the home city 81
End If '82
PathLength = PathLength + Dist_Table(Idx1, Idx2) '83
Next I '84
End Function '85
Some notes on the code:
- Lines 1 to 5 make several variables global in scope. This allows all the routines and all recursions of routine PutCityInSlot to access these variables. Three are the same as in the recursive code, above (Cities, Count and Path), but three are new (ShortPath, ShortDist and Dist_Table), and are used to keep track of distances.
- Lines 6 to 18 are the main routine, called TSP_recursive. It calls four
subroutines to carry out four steps:
- Input_City_Coordinates
- Create_Dist_Table
- PutCityInSlot
- Output_Path
- Lines 19 to 43 are the recursive subroutine PutCityInSlot and its helper function ValidPath. They run through all possible paths. They are the same routines used above but with lines 28 to 32 added to keep track of the shortest path found.
- Lines 44 to 51 are the subroutine Input_City_Coordinates. It reads in the spreadsheet range B3:D12.
- Lines 52 to 60 are the subroutine Create_Dist_Table. It creates a distance table that contains the distance between every pair of cities. To see an example of such a table for towns near the mountain parks of Alberta, Canada, click here.
- Lines 61 to 69 are the subroutine Output_Path. It takes the shortest path found (in the picture it is "172349865"), sorts the cities into that order, and puts the result into range B18:D28. This path is then plotted in a scatter graph.
- Lines 70 to 85 are the function PathLength. This function uses the distance table to calculate the length of a path.
Time Taken to Run the Code
It is interesting to see how long it takes to solve the Travelling Salesman Problem for a given number of cities. We can find out by simply changing line 1 of the code. The vertical axis of the following graph shows the results:
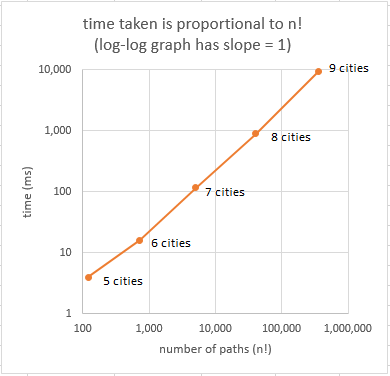
The horizontal axis shows how the number of possible paths varies with the number of cities. For example for 9 cities the time taken is 9500 milliseconds and the number of paths checked is 362,880.
Notice that we have a straight line on a log-log graph. This implies that there is a power law relationship between the time, t, and the number of paths, n! The slope is approximately 1 implying that
r t = n!
The proportionality constant, r, depends on the speed of your computer. For my computer it is about 40,000 paths/second. Let's extrapolate to 12 and 15 cities using this equation. For 12 cities
40,000 t = 12! → t = 11,975 sec = 3.3 hr
For 15 cities it reads
40,000 t = 15! → t = 32,000,000 sec = 1 year
Clearly, it is unrealistic to use this program for more than, say, 12 cities. A completely different idea is to solve the Travelling Salesman Problem approximately using Simulated Annealing, and that is a topic for another blog page.
If you would like to leave a comment or ask a question please send me an email!