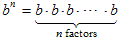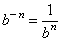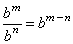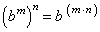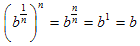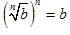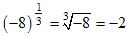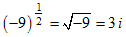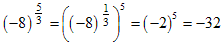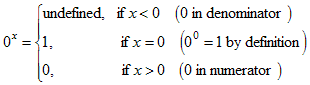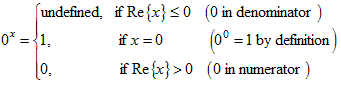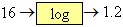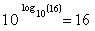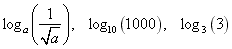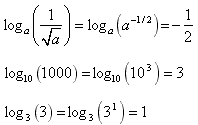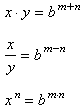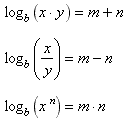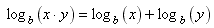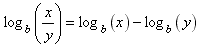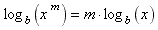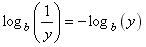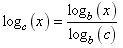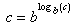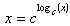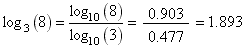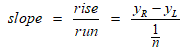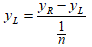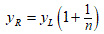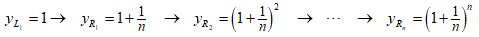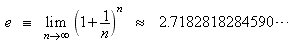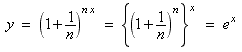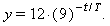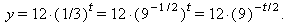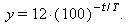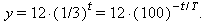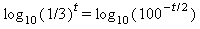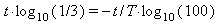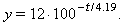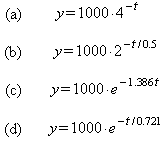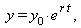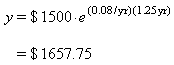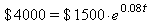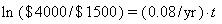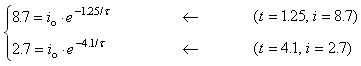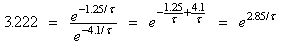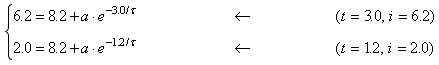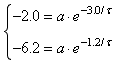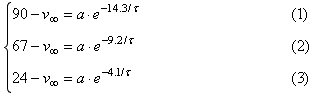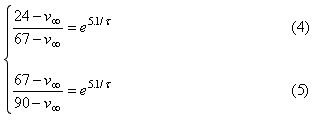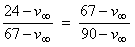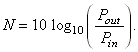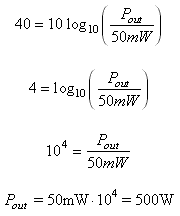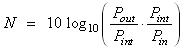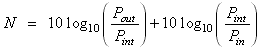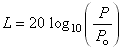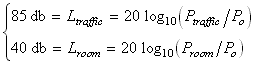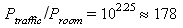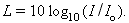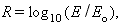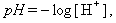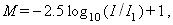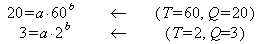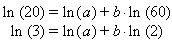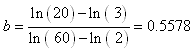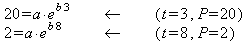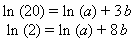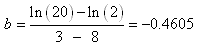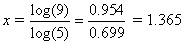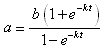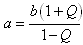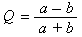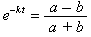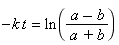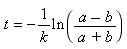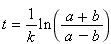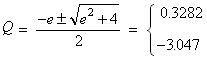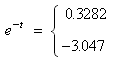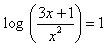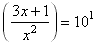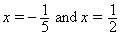Chapter 12 - Exponents and Logarithms
This chapter discusses exponents and logarithms. It contains the following sections:- section 12.1 - In this section we complete
the discussion on the properties of exponents that was begun in
section 3.3 on integer exponents.
- section 12.2 - In this section we
introduce logarithms, state their properties and the change of base formula.
- section 12.3 - In this section we
talk about exponential functions and their various forms.
- section 12.4 - In this section we talk about
logarithmic functions and applications such as decibels and the Richter scale.
- section 12.5 - In this section we talk about
logarithmic and semi-logarithmic graphs.
- section 12.6 - In this section we solve
exponential equations of various types.
- section 12.7 - In this section we solve logarithmic equations.
12.1 - Exponents
Section 3.3 discussed integer exponents. This section continues from there and explains non-integer exponents. We saw that if n is a natural number (i.e. 1, 2, 3, …) then the exponential b n is defined to mean multiplying b by itself n times, like this:The number b is called the base, n is called the exponent, and we say that we are raising b to the n th power. We also saw that any base raised to a negative integer power is the reciprocal of the same base raised to the corresponding positive power:
and that any base raised to the 0th power equals 1:
b 0 = 1.
In that section we also saw that exponentials have these three properties:
Multiplication property 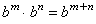
Division property Exponentiation property
Let's assume that these properties can be generalized to exponents that are not necessarily integers. We will find that we can also give meaning to rational and real exponents and even complex exponents.
The meaning of b 1/n : Let m = 1/n in the exponentiation property. This gives:
On the other hand taking the nth power of the nth root of b gives the same result:
Putting this together we find that:
In other words, b 1/n is the nth root of b. The most important case is:
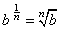
In other words, b 1/2 is the square root of b.
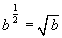
Note: If we are working over the real numbers and the base b is negative then n must be an odd integer; otherwise we can't take the nth root of b. If we are working over the complex numbers then there is no problem and no restriction on n. Click here for more information.
For example the following exponential gives a real value:
but this exponential gives a complex value:
The meaning of b m/n : Using the exponentiation property we can write b m/n two ways:
But in the previous section we saw that b 1/n is the nth root of b. Thus this equation says that b m/n may be thought of as the nth root of the mth power of b or as the mth power of the nth root of b.
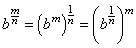
For example:
A note on negative bases: If we are working over the real numbers and the base b is negative then n must be an odd integer; otherwise we can't take the nth root of b. If we are working over the complex numbers then there is no problem and no restriction on n. Click here for more information.
The meaning of b r where r is any real number: We have made sense of exponents that are positive or negative or fractions but what about exponents that are real numbers? We will explain this case using an example. We will show that 10 1.2 equals 16 (approximately). To do this we make a graph of the function y = 10 x. Here is the table of values and the graph with a smooth curve interpolated through the points.
We see that the interpolated curve goes through the point ( x = 1.2, y = 16 ). It is in this sense that we can say that 10 1.2 = 16. It is easy to see that this use of interpolation doesn't depend on the base being 10; any other base would produce a similar result.
Note: If we are working over the real numbers then the base b must be a positive number. If we are working over the complex numbers then the base can have any value, with one exception (namely the base can't be zero if the real part of the exponent is negative or zero, because this causes division by zero; see below.) Click here for more information.
The meaning of 0 x : This is an interesting situation because depending on the exponent x, there is zero either in the numerator or the denominator, so the expression can be either 0 or undefined. And 0 0 cannot be computed; it is defined to equal 1.
In summary, if the exponent x is a real number then there are the following cases:
If the exponent x is a complex number then there are the following cases:
12.2 - Logarithms
Before reading this section you may want to review the previous section on exponents, since logarithms are based on them.Introduction: It is a fact that every positive number, y, can be expressed as 10 raised to some power, x. We write this relationship in equation form, like this:
y = 10 xFor example it is obvious that the number 1000 can be expressed as 10 3, because the exponent 3 means to multiply 10 by itself 3 times and 10·10·10=1000. It is not so obvious that the number 16 can be expressed as 10 1.2. Clearly this cannot mean to multiply 10 by itself 1.2 times! What does it mean and how can we calculate that this is the correct power of 10? We start by giving it a name: logarithm. We say that 1.2 is the logarithm of 16. It is the subject of this chapter.
Let’s start by making a graph of the equation y = 10 x. To make this graph we make a table of a few obvious values of y = 10 x as shown below, left. Then we plot the values in the graph (they are the red dots) and draw a smooth curve through them. Then we observe that the curve goes through y = 16 and x = 1.2 (the black dot). This is what we mean when we say that 16 = 10 1.2.
We next define a function called the logarithm function that takes a number like 16 as input, calculates that it can be expressed as 10 1.2 (click here to see exactly how this is done by your calculator), and returns the exponent 1.2 as its output value:
Here is the formal definition of the logarithm function.
Definition: The logarithm is the function that takes any positive number x as input and returns the exponent to which the base 10 must be raised to obtain x. It is denoted log(x). |
Example 1: Evaluate log ( 10 5.7 ). In this example the argument of the log function (i.e. the quantity in brackets) is already expressed as 10 raised to an exponent, so the log function simply returns the exponent.
log ( 10 5.7 ) = 5.7
Example 2: Evaluate log ( 1000 ). The argument is a number that is easily expressed as 10 raised to an exponent. We do this and the log function then returns the exponent.
log ( 1000 ) = log ( 10 3 ) = 3
Example 3: Evaluate log ( 16 ). The argument is a number which we don't know how to express as 10 raised to an exponent (unless we remember the above discussion which said that 16 = 10 1.2 ). Therefore we use a calculator or the Algebra Coach to evaluate it.
log ( 16 ) = 1.2
Example 4: log ( x + 4 ). The argument is an expression. Until we can evaluate that expression we have no choice but to leave this logarithm as is.
Note that the number 16 can be expressed in exponential form using various bases, so various types of logarithms can be defined. Each type of logarithm is still denoted ‘log’ but we now include the base, written as a subscript, as part of the notation. Here are some examples:
Guided by these examples, we now give the following, more general definition of a logarithm in any base:
16 = 2 4 → log 2 (16) = 4 16 = 4 2 → log 4 (16) = 2 16 = 16 1 → log 16 (16) = 1
Definition: The logarithm to base b is the function that takes any positive number x as input and returns the exponent to which the base b must be raised to obtain x. We denote it as logb(x). |
Notes:
- If the subscript after the word ‘log’ is omitted then the base of the
logarithm is understood to be 10.
Thus log10(x) and log(x) are the same thing.
-
Suppose that x and y are related by the equation
x = b y.
This says that ‘x is b raised to the exponent y’. This is called the exponential form of this relationship. But this same relationship can also be written aslog b(x) = y,
This says that ‘the logarithm of x to base b is y’. This is called the logarithmic form of this relationship. These two equations are equivalent. They are like saying ‘Mary is John’s mother’ and ‘John is Mary’s son’. We say that we are ‘taking logs’ when converting from exponential to logarithmic form, and ‘taking antilogs’ when converting from logarithmic to exponential form.
-
If we substitute the exponential form x = b y into its own
logarithmic form log b(x) = y we get the identity
log b( b y ) = y,
and if we substitute the logarithmic form log b(x) = y into its own exponential form b y = x we get the identity
These identities show how the inverse operations of logging and antilogging undo each other.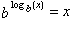
Example: For our previous example 16 = 10 1.2 the above two identities read
log10(10 1.2 ) = 1.2,and
Example: Evaluate each of the following logarithms without using a calculator:
Solution: The key is to express the argument of the log function (i.e. the quantity in brackets) in exponential form with the base chosen to match the base of the log. Then we use the fact that taking logs and exponentiation are inverse operations:
In the above section on exponents we stated these three properties of exponents:
Multiplication property Division property Exponentiation property
If we rewrite them in logarithmic form then they become the properties of logarithms. To do this, make these substitutions on the left side of each of the three properties:
b m = x and b n = yNote for later reference that these substitutions expressed in logarithmic form are:
m = log b(x) and n = log b(y).With the substitutions the three properties of exponents read:
Now take logs of these three equations (i.e. write them in logarithmic form):
Now substitute log b(x) for m and log b(y) for n on the right side of each property (but only for m in the third one). The result is three properties of logarithms.
Examples: For each of the following expressions, use the properties of logarithms (or exponents) to combine the logarithms into a single logarithm:
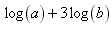
Step 1: get rid of the coefficient 3 by using property 3 to make it an exponent of 3;
Step 2: combine the sum of logs using property 1: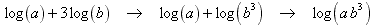
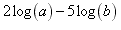
Step 1: get rid of the coefficients 2 and 5 by using property 3;
Step 2: combine the difference of logs using property 2: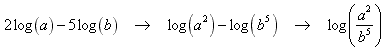
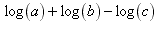
Step 1: combine the sum of the first two logs using property 1;
Step 2: combine the difference of the remaining logs using property 2;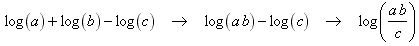
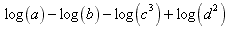
This could be handled exactly the same way as the previous problem but a shortcut is to notice that all positive logs go into the numerator and all negative logs go into the denominator.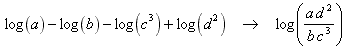
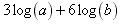
Step 1: get rid of the coefficients 3 and 6 by using property 3;
Step 2: combine the sum of logs using property 1;
Step 3: write a 3 b 6 as (a b 2 ) 3. Click here to see why you can;
Step 4; use property 3 of logarithms again, but this time in reverse:
A shortcut is to notice that a common factor of 3 can be factored out of the two terms at the very beginning: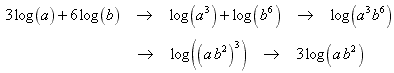
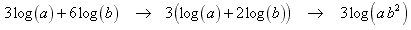
Common logarithms and natural logarithms
Suppose that we wish to express an arbitrary positive number y in exponential form y = b x. The base b that we use could be any positive number whatsoever except 0 or 1. This is because 0x can only equal 0 and 1x can only equal 1 for any value of x. Also, if we try a negative b then we run into trouble with b1/2 since this is the square root of a negative number. Of all the remaining possibilities for the base b there are two special values:-
base b = 10 This would seem to be the obvious choice since our
number system is based on 10 (probably due to the fact that humans
have 10 fingers with which they first learned to count!)
Logarithms to base 10 are called common logarithms.
For convenience we omit the subscript 10 when using common logs.
Thus log(x) is understood to mean log10(x).
All scientific calculators are programmed to compute logarithms to base 10 (on most calculators you use the log button) and antilogs to base 10 (use the 10 x button.)
-
base b = e ≈ 2.71828…
This may not seem like a natural choice for the base but nevertheless logarithms to base
e are called natural logarithms. The importance of base e
(which is the symbol for an irrational number whose value is approximately equal
to 2.718) results from the fact that the exponential growth function
y = e x, with that particular base,
is the only function whose slope equals its own height everywhere.
This makes it important in the study of any quantity whose rate of growth is
proportional to its present value. (An example is the balance in an interest
bearing bank account.)
Click here for more information on the function
y = e x.
For convenience we will use the abbreviation ln(x) instead of the longer
form log e(x) to represent the natural logarithm
function. (LN stands for Log Natural.)
All scientific calculators are programmed to compute logarithms to base e (on most calculators use the ln button) and antilogs to base e (use the e x button.)
Here is a comparison table for common logarithms and natural logarithms:
Common logarithms Natural logarithms the base 10 e ≈ 2.718 an example in exponential form y = 10 3 = 1000 y = e 3 ≈ 20.08 the same example in logarithmic form log(y) = 3 ln(y) = 3
The Change of Base Formulas
Logarithms to base 10 and logarithms to base e are proportional to each other (just like miles and kilometers). Logarithms in one base can be changed to logarithms in any other base using a ‘change of base formula’ which basically just uses a proportionality constant. There is also a change of base formula that can be applied to a relationship expressed in exponential form.Logarithmic form of the Change of Base Formula: Exponential form of the Change of Base Formula: These formulae are used to convert from an inconvenient base c to a convenient base b (usually 10 or e). The left side is usually converted to the right side. The quantity log b(c) is the conversion factor. |
Proof: To prove the second formula notice that it is just the identity discussed previously, namely
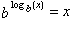 , with x replaced
by c. To prove the first formula, start with the second formula in the form:
, with x replaced
by c. To prove the first formula, start with the second formula in the form:
and follow these steps:
Example: Compute log 3 (8).
Solution: Use the logarithmic form of the change of base formula:
Example: Express the function y = 7 x using the base e instead of the base 7.
Solution: Use the exponential form of the change of base formula on the number 7. Remember that ln(7) means the same thing as log e(7).
7 = e ln (7) = e 1.946Substitute this expression in for 7 in y = 7 x.
y = (7) x = (e 1.946 ) x = e 1.946 x
12.3 - Exponential Functions
Click here to review the definition of a function. Click here to see how exponential functions compare with other types of functions in the gallery of functions.Exponential functions are closely related to geometric sequences. A geometric sequence is a list of numbers in which each number is obtained by multiplying the previous number by a fixed factor m. An example is the sequence {1, 3, 9, 27, 81, …}. If we label the numbers in the sequence as {y0, y1, y2, …} then their values are given by the formula
yn = y0 · m n.
A geometric sequence is completely described by giving its starting value
y0 and the multiplication factor m.
For the above example y0 = 1 and m = 3.
Another example of a geometric sequence is the sequence {40, 20, 10, 5, 2.5, …}.
For this sequence y0 = 40 and m = 0.5.
An exponential function is obtained from a geometric sequence
by replacing the counting integer n by the real variable x.
The graph below shows the exponential functions corresponding to these two geometric sequences.
Thus we define an exponential function to be any function of the form
y = y0 · m x.It gets its name from the fact that the variable x is in the exponent. The “starting value” y0 may be any real constant but the base m must be a positive real constant to avoid taking roots of negative numbers.
The exponential function y = y0 · m x has these two properties:
- When x = 0 then y = y0.
- When x is increased by 1 then y is multiplied by a factor of m.
This is true for any real value of x, not just integer values of x.
To prove this suppose that y has some value ya
when x has some value xa.
That is,
Now increase x from xa to xa + 1. We get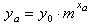
We see that y is now m times its previous value of ya. If the multiplication factor m > 1 then we say that y grows exponentially, and if m < 1 then we say that y decays exponentially.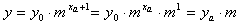
The Graph of the Exponential Function
We have seen graphs of exponential functions before:- In the section on real exponents we saw a saw a graph of y = 10 x.
- In the gallery of basic function types we saw five different exponential functions, some growing, some decaying.
Notice that the two curves have the same general shape but are reversed left to right and that neither ever touches the x axis. Notice also that if we interchange the x and y axes then the graph of an exponential function turns into the graph of a logarithmic function. The reason for this is that if we take the exponential function y = b x, then interchange x and y to get x = b y, and then solve for y we get y = log b(x).
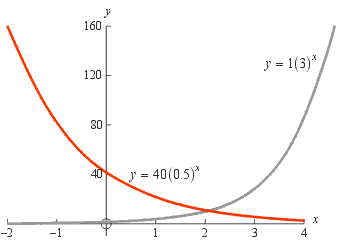
The Special Propery of y = e x
We have seen graphs of various exponential functions y = b x with various bases b. Notice that for all of them, as we go higher and higher up the curves, they get steeper and steeper. Of all the possible bases there is one particular base, namely e, that causes the curve to have the property that the slope exactly equals the height at every point along the curve. This property defines the number e and makes the curve y = e x an important standard in calculus where we study the slopes of different functions.

Let’s prove this important property.
Constructing the Function y = e x
In this section we will construct a function whose slope equals its own height everywhere and then show that it is indeed the function y = e x.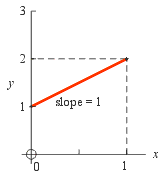
We begin in the figure to the right with a single straight-line segment whose left endpoint is at (x = 0, y = 1). Since the height there is 1 we demand that the slope equal 1. The problem of course is that this line segment rises to the right but the slope is not increasing as it should if we wish the slope to equal the height everywhere along the curve.
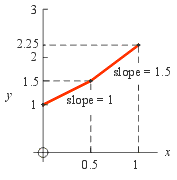
So we improve on this by dividing the region 0 < x < 1 into two equal intervals as shown here. At x = 0.5 we change the slope to 1.5 to reflect the fact that the height there is 1.5. Now the slope equals the height at two points, namely the left endpoints of both line segments.
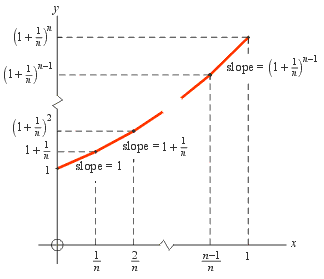
Now we improve even more by dividing the region 0 < x < 1 into n equal intervals as shown here. We can find the height of the right endpoint of each line segment by the following method:
Start with the formula for the slope of any line segment.
In this formula yR is the height at the right endpoint and yL is the height at the left endpoint of the line segment. Now we demand that the slope of each line segment equals the height of its left endpoint. Substitute this in.
Now solve for yR.
Knowing yL we can use this formula to find the yR. We can iterate this formula across all n line segments, working from left to right. The heights of the right endpoints of all n line segments work out to be:
These heights are shown in the third figure. Now we let n → ∞ (i.e. we let the number of intervals become infinite). The curve will become smooth and the slope will equal the height everywhere. We claim that the resulting curve is the function y = e x. To prove this let’s first find the value of y at x = 1. The third figure says that this value is (1 + 1 / n) n. In the following table we have used a calculator to find the value of the expression (1 + 1 / n) n for various values of n:
n (1 + 1 / n) n 1 2 2 2.25 10 2.59374 1000 2.71692 1,000,000 2.71828
The values are approaching a definite limit as n becomes large. We define the number e to be the value of the expression (1 + 1 / n) n in the limit as n → ∞. (The number is named e in honor of Leonard Euler who first discovered it.) We express this using this notation:
Now let’s find the value of y at arbitrary x. We must begin at x = 0 and go right a total of n · x intervals or steps. From the figure above it is clear that the value of y after n x intervals is y = (1 + 1 / n) n x. By the rules of exponents this can be written
in the limit as n → ∞. Thus the function whose slope equals its own height everywhere and which goes through the point (x = 0 , y = 1) is y = e x as claimed.
Summary: The function y = e xis the function whose slope equals its own height everywhere and which goes through the point (x = 0 , y = 1). |
Generalization: The function y = y0 · e bxis the function whose slope is b times its own height everywhere and which goes through the point (x = 0 , y = y 0 ). (b may be positive or negative.) |
This generalization can be understood as follows:
- The function y = y0 · e x
is just the function y = e x but stretched vertically
by the factor y0. Thus both its slope and height are everywhere multiplied by the
factor y0. Its slope still equals its own height everywhere but it goes through
the point (x = 0 , y = y0) .
- The function y = y0 · e bx is just the function y = y0 · e x but squeezed horizontally by the factor b. Thus its slope is everywhere multiplied by factor b but its height is not changed.
Alternative Forms for Exponential Growth and Decay
Let us now replace the independent variable x in the exponential function by the variable t and let it represent time. Now the exponential function looks like this:y = y0 · m t.We already know that y has the value y0 when t = 0 and that y is multiplied by a factor m when time t is increased by 1. If m > 1 then y grows with time and if m < 1 then y decays with time. We call the growth or decay exponential because t is in the exponent. We have seen how we can change the base by using the change of base formula. In this section we want to show how using various bases or putting the exponent in various forms can reveal various features of the exponential growth or decay.
Form 1: Base Greater than 1. First, we can always choose the base m to be greater than 1. The reason for doing this is that then
y = y0 · m+ t,with positive exponent makes it obvious that we have exponential growth, and
y = y0 · m− t,with negative exponent makes it obvious that we have exponential decay. The growth or decay is by the factor m each time t increases by 1. For example the function y = (¼) t describes exponential decay but the base is smaller than 1. But using the rules of exponents we can rewrite it as y = (4−1) t, or as
y = 4 − t.Now the base is bigger than 1 and the exponent is negative. Notice that these two forms show that the statements “y is multiplied by a factor of 1/4 ” and “y decays by a factor of 4 ” are equivalent.
Form 2: Growth or Decay by Given Factor in Given Time. Next we want to give t units, say seconds. To do this we can write an exponential growth in the form
y = y0 · b t / T,where b again is a base > 1, and T is a positive constant with the same units of time as t. This form is useful because it makes it plain that y grows by a factor b in a time of T seconds as we can see from this table of values:
t y0 · b t / T 0 y0 · b 0 = y0 T y0 · b T / T = y0 · b 2 T y0 · b 2 T / T = y0 · b 2
Note: We can always change b but we must change T accordingly. For example exponential growth by a factor of 10 every 1 second is equivalent to growth by a factor of 100 every 2 seconds.
Similarly, any exponential decay can be written as
y = y0 · b − t / T,making it plain that y decays by a factor b in a time of T seconds.
Form 3: The Time Constant Form. This is a special case of Form 2. If b = e then the constant T is called the time constant and is denoted by the greek letter τ (tau). The exponential growth formula now reads
y = y0 · e+ t / τ,making it plain that y grows by a factor of e or approximately 2.7 every τ seconds. The decay formula reads
y = y0 · e − t / τ,making it plain that y decays by a factor of e or approximately 2.7 every τ seconds (or decays to e − 1 ≈ 37% of its former value every τ seconds). This can be seen from the table of values:
t y0 · e − t / τ 0 y0 · e 0 = y0 τ y0 · e − τ / τ = y0 · e − 1 ≈ 37% of y0 5 τ y0 · e − 5 τ / τ = y0 · e − 5 ≈ 0.7% of y0
Electrical engineers prefer this form because τ is easy to measure and to calculate.
Summary: The time constant τ is the period of time that it takes for an exponentially decaying quantity to decay to a fraction e − 1 of its initial value, or to about 37% of its initial value. After a period of 5 time constants it has decayed to less than 1% of its initial value and for many engineering purposes equals zero. |
Form 4: The Rate Form. Any exponential growth can be written in the form
y = y0 · e+ r t.Comparing this with the time constant form we see that r = 1 / τ. Assuming τ has units of seconds, then r has units of 1/seconds. r is called the instantaneous growth rate. Bankers and people interested in rates of growth prefer this form. The equation y = y0 · e+ r t represents a quantity y whose initial value is y0 and whose rate of growth at any instant equals r times its value at that instant.
Similarly any exponential decay can be written in the form
y = y0 · e − r t,This equation represents a quantity y whose initial value is y0 and whose rate of decay at any time equals r times its value at that time.
Example: Describe the function y = $50 · e 0.20 t in words and sketch its graph. Assume that t is measured in years.
Solution: This is an exponential growth function expressed in rate form. Its value is $50 at time 0 and it grows at a rate of 20% per year. In the sketch below we have shown that the slope of the curve is 0.20 times the height at three different points along the curve.
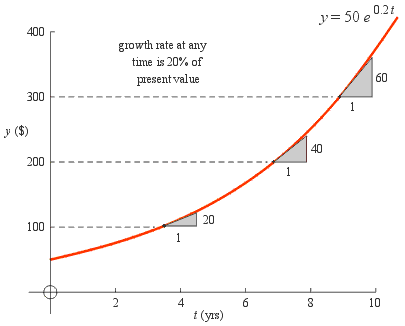
Example: Describe the function y = 100 · e − t / 1.5 and sketch its graph.
Solution: This is an exponential decay function expressed in time constant form. Its value at time 0 is 100 and it decays to 37% of its former value in any 1.5 second interval. In the sketch we have shown this for two different intervals.

Example: Take the exponential function y = 12 · (1/3) t and put it into the “decay by a given factor in a given time” form which will show at a glance how long it takes
a) to decay by a factor of 9, andSolution:
b) to decay by a factor of 100.
a) We wish to change the base to 9 so the formula reads
Then the value of T will be the time required to decay by the factor of 9. Notice that 1/3 = 9 −1/2. Substituting this into the original exponential function gives
This form clearly shows that y decays by a factor of 9 every 2 seconds.
b) We wish to change the base to 100 so the formula reads
No simple short-cut with exponents is possible in this case. Instead we can equate the given original form for y with the desired form. This gives
We must solve this equation for T. To do this divide by 12 and take log 10 on both sides
Use property 3 of logarithms to bring down to exponent:
Now divide both sides by t and solve for T. We get
T = 4.19 seconds.Substituting this into the desired form gives
This form clearly shows that y decays by a factor of 100 every 4.19 seconds.
Example: Consider the function y = 1000 · (1/4) t which is graphed below:
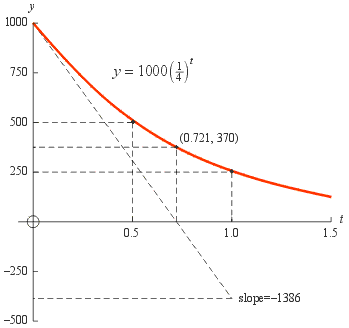
Using the exponential form of the change of base formula and some simple algebra it is possible to rewrite this function in the following equivalent forms:
Discuss the merits of each of the forms.
Solution:
All of the forms have a base greater than 1 so the negative exponent indicates exponential decay (as opposed to growth). All of the forms have y with an initial value of 1000.
- Form (a) shows that y decays by a factor of 4 each time t increases by 1
second.
- Form (b) shows that y decays by a factor of 2 each time t increases by
0.5 sec.
- Form (c) shows that y decays at an instantaneous rate of 138.6% per second.
(The dashed triangle in the figure shows that at the initial value of 1000 this
implies an initial slope of −1386.)
- Form (d) shows that y decays by a factor of e (or decays to 1/e ≈ 37% of of its former value) each time t increases by 0.721 sec. In other words y decays with a time constant of 0.721 sec.
Example: Suppose that we put $1500 into a bank account which receives interest at a rate of 8% per year and which is compounded continuously. (Compounded continuously is just another way of saying grows exponentially.) Let y denote the amount of money in the account at any time t. Then y can be expressed in the rate form
where y0 = $1500 is called the principal and r = 0.08/yr is the interest rate. The units of y will also be dollars and t must be given in years so that the units of r and t cancel. Questions:
(a) What amount will be in the account at the end of 15 months?Solution:
(b) After how many years will there be $ 4000 in the account?
(a) Substituting t = 15 months = 1.25 yrs into the equation and evaluating gives
(b) Substituting y = $4000 into the equation and solving for t gives
t = 12.26 yrs.Answers:
(a) After 15 months the account holds $ 1657.75.
(b) The account holds $ 4000 after 12.26 yrs.
Example: Make a sketch of the exponential decay function y = 45 · e − t / 20
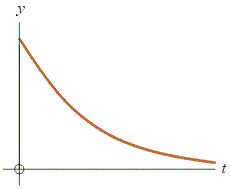 Solution: Follow these steps:
Solution: Follow these steps:(a) Draw a smooth decay curve from upper-left to lower-right. Label the axes but don’t put any numbers on the axes yet.
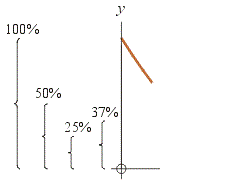
(b) Draw a bracket (or just imagine it) to indicate where y has 100% (or all) of its initial value. Then draw brackets ½ and ¼ as high where y has 50% and 25% of its initial value. About half-way between 25% and 50% lies 37%. Remember that e−1 is about 37%.
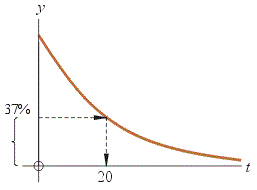
(c) Go across at 37% until you hit the curve then go down. This value on the t axis is the time constant. Our function has a time constant of 20 so put that on the t axis.
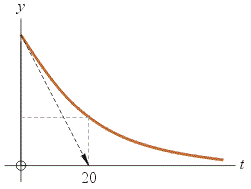
(d) Accuracy check: a straight line with the initial slope should hit the same spot on the t axis.
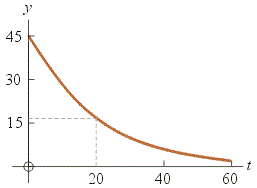
(e) Finish up the graph by putting more tick marks and values on both axes.
Analyzing Exponential Growth and Decay
Just as 2 points determine a straight line, so 2 points determine an exponential function. To derive its equation follow these steps:- choose the desired form of the equation,
- substitute in the 2 points, and
- solve the resulting 2 equations for the 2 unknowns, one being the initial value and the other being the growth or decay rate or time constant.
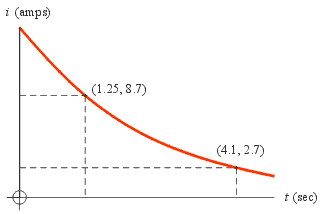
Example: The electric current, i, flowing in a certain electric circuit decays exponentially with time, t, as shown. Two points on the curve are given. Find an exponential equation of the time constant form
i = i0 · e − t / τto describe the current.
Solution: We will explain two methods of solving this problem.
Method 1: Substitute the values of i and t at the 2 given points into the equation. This yields a system of 2 equations in the 2 unknowns. The unknowns are i0 and τ:
We can eliminate i0 by dividing these equations
Take the natural logarithm of both sides and solve for τ
ln(3.222) = 2.85 / τNow back-substitute this value of τ into, say, the first of the two equations to get i0:
τ = 2.436
8.7 = i0 · e − 1.25 / 2.436Thus the equation is i = 14.5 · e − t / 2.44.
i0 = 14.5
Method 2: This method uses the fact that an exponential function decays by a given factor in a given time anywhere along the curve. Thus for the purposes of finding the time constant τ we may use the value 8.7 as i0 and the time difference 4.1 − 1.25 = 2.85 sec. as the time taken for the function to decay to the value 2.7. Substituting these numbers into the equation yields
2.7 = 8.7 · e − 2.85 / τThis equation can be solved for τ
τ = 2.436Now get the actual i0 by substituting τ and one of the points on the curve, say (t = 1.25, i = 8.7), into the equation i = i0 · e − t / τ to get:
8.7 = i0 · e − 1.25 / 2.436Thus again we find the equation to be i = 14.5 · e − t / 2.44.
i0 = 14.5
Exponential Decay Toward a Limiting Value
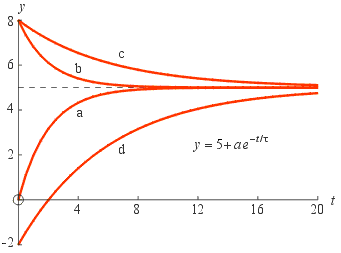
The figure to the right shows four functions whose differences from the limiting value y = 5 decay exponentially at various rates. The functions are:
(a) y = 5 − 5 e − t / 2
(b) y = 5 + 3 e − t / 2
(c) y = 5 + 3 e − t / 6
(d) y = 5 − 7 e − t / 6
These functions could describe the temperature of hot drinks cooling and cold ones warming toward room temperature. (c) and (d) are in better insulated containers so they take longer to heat or cool. These functions are all of the form
y = y∞ + a e − t / τ,There are 3 parameters: y∞ , a and τ. If we write transpose y∞ to the left-hand-side and write the equation as
y − y∞ = a e − t / τ,then we see that the right side is the familiar exponential decay in time constant form, and that the difference of y from y∞ equals a when t = 0 and that this difference decays with time constant τ. When t = ∞ then y = y∞. Because there are 3 parameters, we must be given the value of y at 3 different times to fix them.
We look at two examples. In this first example the limiting value is given so we only need 2 more points.
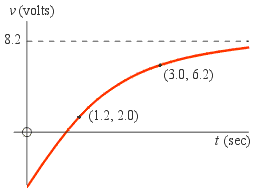
Example: The voltage in a certain electric circuit decays exponentially toward the limiting value v∞ = 8.2. Two points on the curve are given. The curve may be described by an equation of the form
v = v∞ + a e − t / τ,Calculate the values of a and τ.
Solution: Similar to the previous example, there are two methods of solving this problem.
Method 1: Substitute v∞ = 8.2 and the values of v and t at the 2 given points into the equation. This yields a system of 2 equations in the 2 unknowns a and τ:
In the previous example we divided one equation by the other in order to eliminate one of the variables. Here we must first move the 8.2 to the left-hand-side:
Now we can divide the equations. We get
0.3226 = e −1.8 / τSolving gives τ = 1.591 and back-substituting gives a = −13.18.
Method 2: In this method use the fact that the difference of v from v∞ decays exponentially to find the time constant τ first. At the first point this difference is 6.2, and 1.8 seconds later the difference is 2.0. Substituting these values into the time constant form of the exponential decay formula, y = y0 e − t / τ, gives
2.0 = 6.2 e − 1.8 / τSolving for τ gives
τ = 1.591Now find the value of a by substituting τ, v∞ and the value of t and v at either one of the given points into the equation v = v∞ + a e − t / τ. This again gives a = −13.18.
In this second example we are given 3 points separated by equal time intervals. If the time intervals were unequal the resulting system of equations could only be solved by computer.
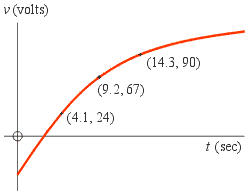
Example: The curve to the right is described by the equation
v = v∞ + a e − t / τ,Calculate the values of v∞ , a and τ accurate to 3 significant figures.
Solution: Move v∞ to the left-hand-side as we did in the previous example. Then substitute in the values of v and t at the 3 given points. This yields the following system of 3 non-linear equations in the 3 unknowns v∞ , a and τ:
We can eliminate a by dividing Eq.(3) by (2), and (2) by (1), to get:
Now we can eliminate τ by equating Eqs.(4) and (5). (Note that they are equal only because the 3 points were separated by equal time intervals.) We get
After cross-multiplying we can solve to get v∞ =116.45 volts. Substituting this back into Eq.(4) or (5) we get τ = 8.151 secs and substituting this back into Eq.(1), (2) or (3) we get a = 152.9 volts, so the final equation to 3 sig. figs. is
v = 116 − 153 e − t / 8.15.
12.4 - Logarithmic Functions
Click here to review functions. Click here to see how logarithmic functions compare with other types of functions.Logarithmic functions are often used to describe quantities that vary over immense ranges. Large ranges of numbers occur in many settings: the amplification abilities of different electronic amplifiers, the sensitivity range of the human eye or the human ear, or the range of energies released by earthquakes. Logarithmic scales such as the decibel scale and the Richter scale are designed to describe large ranges of numbers.
Any logarithmic function can be expressed in the form:
y = a ln (x) + b,where x and y are variables and a and b are constants. An example is:
y = 2.79 ln (x) + 5.80.This function can be expressed in many equivalent forms using the change of base formula. For example:
y = 2.79 ln (x) + 5.80
= 6.43 log (x) + 5.80
= 5 log 6 (8 x).
The Graph of the Logarithmic Function
Here are graphs of the functions y = log (x) and y = ln (x).
Notice that immense variations in x correspond to small changes in y (at least in the region x > 1). Notice also that log(0) = −∞, and that logarithmic functions exist only to the right of the y axis. Thus the logarithm of a negative number does not exist. The graph of any logarithmic function has the same shape as these and will differ only in a vertical shift and/or a vertical stretch.
The Electromagnetic Spectrum
The electromagnetic spectrum is mentioned here because it is a nice example of a logarithmic scale.Electromagnetic (EM) waves can be produced and detected in a variety or spectrum of wavelengths. The table below shows the EM spectrum and the names given to EM radiation of various wavelengths. The spectrum is actually infinite - we have simply shown the range from 10 −15m to 10 6m that has been intensively exploited by mankind so far.
The scale used to present the wavelengths is called a logarithmic scale. In this type of scale each factor of 10 in wavelength is allocated one line of the table. That is, the range from 10 1 to 10 2 is allocated the same amount of space as the range from 10 2 to 10 3, namely 1 line. By contrast in a linear scale the range from 10 2 to 10 3 (a range of 900) would be allocated 10 times as much space as the range from 10 1 to 10 2 (a range of 90).
wavelength
(in meters)name of region of
EM spectrum10 −15 10 −14 10 −13 gamma ray 10 −12 10 −11 10 −10 x-ray 10 −9 10 −8 10 −7 ultraviolet 10 −6 visible region 10 −5 infrared 10 −4 10 −3 10 −2 microwave 10 −1 10 0 short radio waves 10 1 FM radio 10 2 AM radio 10 3 10 4 10 5 long radio waves 10 6
Here is a brief history of the electromagnetic spectrum and the significance of some of its regions. In 1820 Oerstad and Ampere discovered that any wire carrying an electric current was surrounded by a magnetic field. A practical application of this effect was the electromagnet. In 1831 Michael Faraday discovered that a changing magnetic field near a wire could induce a voltage in the wire. A practical application of this effect was the electric generator.
In 1865 James Clerk Maxwell was able to combine the mathematical equations describing these two effects and to theoretically predict the existence of waves of electricity and magnetism, which we now call electromagnetic (EM) radiation. His equations also predicted the velocity of these waves. You can imagine his excitement when he discovered that their speed was exactly the speed of light! Twenty-two years later Hertz first produced and detected electromagnetic waves, and ten years after that Marconi invented the radio.
Our eyes are sensitive only to a very small part of the EM spectrum called the visible region. Different wavelengths in this region are perceived by us as the different colors of the rainbow. Visible light is caused by transitions of the outermost electrons of atoms from one orbit to another.
We feel as heat on our skin (rather than see) the infrared region of the EM spectrum. And our skin becomes tanned by ultraviolet radiation.
EM radiation from the microwave region causes the water molecule to vibrate. This effect can be used to cook food in a microwave oven. (In case you wondered, the metal screen on the oven door has a fine enough mesh to short circuit the electric component of the microwaves so they can't escape from the oven but is coarse enough to let the shorter wavelength visible light through so that we can see what's cooking inside.)
X-rays are emitted by the inner electrons of atoms as they fall from a higher orbit to a lower one. Gamma rays are caused by the rearrangement of particles inside an unstable atomic nucleus.
The energy of radiation depends on two things: the intensity (brightness) of the radiation, and the wavelength; short wavelengths being more energetic than long wavelengths. Thus gamma rays are the most energetic and dangerous form of radiation.
Astronomy is one area of science that uses every part of the EM spectrum. Radio telescopes as big as several kilometers across gather the long-wavelength radiation emitted by molecules in interstellar space. X-ray telescopes (launched into earth orbit to avoid absorption of x-rays by the earth's atmosphere) observe short-wavelength radiation emitted by black holes, neutron stars and other exotic objects.
The Decibel Power Scale
An ideal amplifier multiplies the height of an input signal by some factor and outputs it without distortion.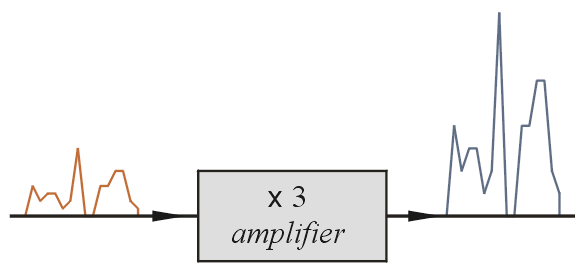
If the height of the signal represents power then the amplification factor is the ratio Pout /Pin where Pout is the output power and Pin is the input power, both measured in Watts at the same instant in time. For lasers the ratio can be up to 10 12. Attenuators, of which microphones are an example, are devices for which the ratio Pout /Pin is much less than 1. To compress these large variations we define the decibel scale:
N is called the gain of the amplifier or attenuator. It is measured in units called decibels (abbreviated db). Notice that the gain is positive for amplifiers, negative for attenuators and zero if Pout /Pin = 1.
Example: What is the output power Pout of an amplifier with a gain of 40 db if Pin = 50 mW?
Solution: Substitute the given values into the gain formula and then solve for Pout :
Amplifiers in Cascade: To achieve very large amplification factors amplifiers are cascaded, which means that the output of one amplifier becomes the input of the next amplifier:
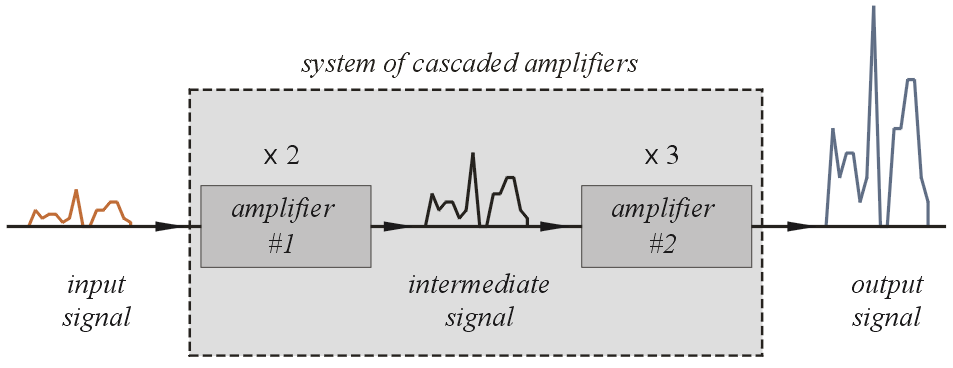
The amplification factor of the whole system is the product of the amplification factors of the components. The whole system in the figure has an amplification factor of 6. Equivalently, the gain of the system equals the sum of the gains of its components. To prove this statement let Pin be the power going into amplifier # 1, Pout be the power coming out of amplifier # 2 and Pint be the intermediate power (coming out of Amplifier # 1 and going into # 2). The gain of the whole system is:
Now put a factor of Pint /Pint inside the brackets:
Now use property 1 of logarithms:
The first term in the final expression is just the gain of amplifier # 2 and the second term is the gain of amplifier # 1. This proves that the gain of a system equals the sum of the gains of its components.
Example: Find the output power of the system shown:

Solution: Adding the three gains gives the gain of the whole system, N = 45 db. Therefore:
45 = 10 log 10 (Pout / 0.05W)Solving for Pout gives:
Pout = 0.05 W · 10 4.5 = 1581 W
Sometimes the gain formula is used to compare the signal power to the noise power. For example a signal-to-noise ratio of 1000:1 may be quoted as +30 db.
The Decibel Loudness Scale
Fluctuations in air pressure cause our eardrums to vibrate and we interpret these vibrations as sound. The loudness L of a sound (measured in decibels) is defined as:where P is the pressure fluctuation of the sound and Po is the pressure fluctuation of a sound at the threshold of human hearing, which is 20 μPa.
Example: How many times larger are the pressure fluctuations of average traffic noise (with a loudness of 85 db) than average livingroom noise (with a loudness of 40 db)?
Solution: Substituting each noise into the loudness formula, we have:
We can eliminate Po and compare Ptraffic and Proom directly by subtracting these equations and using property 2 of logarithms:
Solving for the ratio Ptraffic /Proom gives:
The acoustic loudness scale can also be defined in terms of the intensity I of the sound (the energy/unit area/unit time falling on the eardrum):
The threshold intensity for human hearing is Io = 10 −12 Watts / m2. A factor of 10 appears in this formula (rather than 20) since the energy of a wave is proportional to the square of the pressure fluctuation.
The Richter Earthquake Scale
The Richter number R describing the strength of an earthquake is defined as:where E is the energy released by the earthquake and Eo is a reference arbitrarily set at the limit of sensitivity of Richter's original seismic measuring apparatus.
The pH Acidity Scale
The pH number of an acid or base is defined as:where [ H + ] is the concentration in moles/liter of the H + ion responsible for acidity. A solution with pH = 7 is neutral, pH < 7 is an acid and pH > 7 is a base.
The Astronomical Brightness Scale
The magnitude M of a star describes its brightness as it appears to us on earth and is defined as:where I is the intensity of the light from the star. I1 is the intensity of a first magnitude star (the 20 brightest stars in the sky are approximately magnitude 1). The most powerful telescopes can detect stars as faint as magnitude +24.
12.5 - Logarithmic Graphs
In section 6.1 we learned about the cartesian plane, rectangular coordinates, graphs and how to identify points on graphs. Before reading this section you may want to review that section.Henceforth we will call the graphs described in section 6.1 linear graphs. In this section we will learn how to plot quantities on a new type of graph called a logarithmic graph. We will see how this can make it easier to determine the functional relationship between certain quantities.
We will motivate logarithmic graphs by giving two examples.
| t | i | ln(i) |
| 0.00 | 5.00 | 1.64 |
| 2.00 | 2.57 | 0.94 |
| 4.00 | 1.32 | 0.28 |
| 6.00 | 0.68 | -0.39 |
| 8.00 | 0.35 | -1.05 |
| 10.00 | 0.18 | -1.71 |
Find an equation relating i and t.
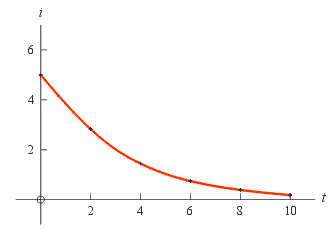 Solution: First we try plotting i versus t.
But this only produces a curve as shown to the right and from this curve it is difficult to find the equation.
Solution: First we try plotting i versus t.
But this only produces a curve as shown to the right and from this curve it is difficult to find the equation.
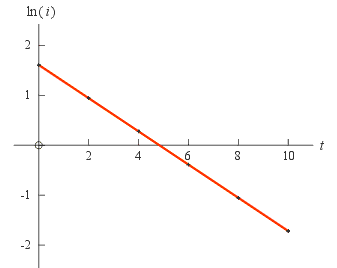 Next we try plotting ln (i) versus t.
This does produce a straight line as shown to the right
and we know how to find the equation of a straight line.
Next we try plotting ln (i) versus t.
This does produce a straight line as shown to the right
and we know how to find the equation of a straight line.To find the equation of this line we will pretend for a moment that the axes are labelled y and x. Then this line must have the equation y = m x + b, where m and b are yet to be determined. Eventually we’ll put back the proper label ln (i) for y and t for x.
To determine m and b we will use the elimination method discussed in section 6.2. Let’s use these two points which lie on the line:
(x = 2.00 , y = 0.94) and (x = 8.00, y = −1.05).Substituting the first point into the equation of the straight line, y = m x + b, gives the equation
0.94 = 2 m + b.Substituting the second point into the equation of the straight line, y = m x + b, gives the equation
−1.05 = 8 m + b.This pair of equations,
0.94 = 2 m + bis a system of two equations for the two unknowns m and b. We can solve them by elimination. Subtracting the first equation from the second equation eliminates b and gives:
−1.05 = 8 m + b
−1.99 = 6 mBack-substituting this value of m into, say the first equation, 0.94 = 2 m + b, then gives 0.94 = (2)(−0.33) + b which gives b = 1.6. So the equation of the straight line ism = −0.33
y = −0.33 x + 1.6.Now replace back y by ln(i) and x by t:
ln (i) = −0.33 t + 1.6.Antilogging this equation gives the equation
i = e −0.33 t + 1.6,or simplifying,
i = 5 e −0.33 t.
The key lesson learned from this example is that the graph of any exponential function y = a e b x is a straight line when we plot ln (y) versus x. |
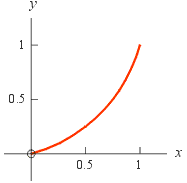
Example 2: The curve to the right could be the graph of y = x 2, y = x 3 or y = x 4. From a plot of y versus x it is difficult to tell which it is.
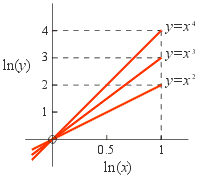
But if we plot ln (y) versus ln (x) then these three functions become straight lines. These functions are called power functions because the variable x is raised to some power.
The key lesson learned from this example is that the graph of any power function y = a x b is a straight line when we plot ln (y) versus ln (x). |
Semilog And log-log graph paper
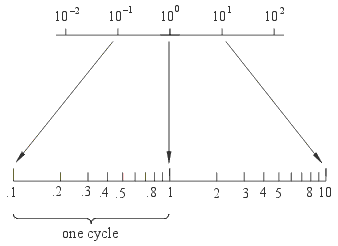
The figure above shows a logarithmic scale of the kind used on logarithmic graph paper. It is not a linear scale because larger numbers are allotted less space than smaller numbers. The lower part of the picture shows the logarithmic scale in more detail. The numbers along the axis are located where their logarithms would be placed on linear graph paper. This means that we can plot x itself on logarithmic graph paper rather than plot log (x) on linear graph paper. We avoid the job of taking logarithms on the calculator. Notice that moving to the left along a logarithmic axis only makes the numbers smaller and smaller. Zero is located an infinite distance to the left and negative numbers do not exist. The range from one power of 10 to the next is called a cycle.
Two types of logarithmic graphs are useful:
the semi-log graph, which has a logarithmic vertical scale and a linear horizontal scale, as shown below. the log-log graph, which has a logarithmic vertical scale and a logarithmic horizontal scale, as shown below.
The equations of straight lines on logarithmic graph paper
One purpose of logarithmic graph paper is simply to put wide ranges of data on one graph. Another purpose is to quickly check if a function follows an exponential law or a power law. We saw one example showing that plotting ln (y) versus ln (x) caused power law functions of the form y = a x b to become straight lines. And we saw another example showing that plotting ln (y) versus x caused an exponential function of the form y = a e b x to become a straight line. From these two examples we conclude the following:
|
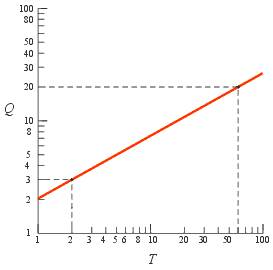 Example: Find the equation of the straight line in the graph to the right.
Example: Find the equation of the straight line in the graph to the right.Solution: A straight line on a log-log graph of Q versus T represents the power law function
Q = a T b.We must find the values of a and b. To do this we will use a variation of the method described in section 6.2.
Take the two points shown in the graph and substitute them, one at a time, into the equation Q = a T b. This gives two equations in the two unknown constants a and b:
Here is the variation: first take natural logarithms of both equations
and then subtract the two equations. This eliminates ln (a). Then solve for b:
Note that b is the power of the power function and is often called the “slope of the log-log graph” and this equation is often used as a shortcut to compute it.
Back-substituting b into either of the previous equations gives ln (a) = 0.7120, and anti-logging gives a = 2.04. The constant a is often called the “intercept” although it occurs at T = 1, not at T = 0. (Remember that 0 does not exist in a logarithmic scale.)
So to 3 sig. figs. the equation describing the line is
Q = 2.04 t 0.558.
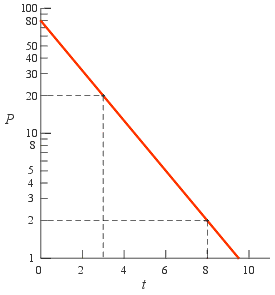 Example: Find the equation of the straight line in the graph to the right.
Example: Find the equation of the straight line in the graph to the right.Solution: A straight line on a semi-log graph of P versus t represents the exponential function
P = a e b t.We must find the values of a and b. To do this we will use a variation of the method described in section 6.2.
Take the two points shown in the graph and substitute them, one at a time, into the equation P = a e b t. This gives two equations in the two unknown constants a and b:
Here is the variation: first take natural logarithms of both equations
and then subtract the two equations. This eliminates ln (a). Then solve for b:
Note that b is the rate of the exponential function and is often called the “slope of the semilog graph” and this equation is often used as a shortcut to compute it.
Back-substituting b into either of the previous equations gives ln (a) = 4.377, and anti-logging gives a = 79.6. Note that the constant a is the “y intercept”. So to 3 sig. figs. the equation describing the line is
P = 79.6 e −0.461 t.
12.6 - Exponential Equations
Before reading this section you may find it helpful to review the following topics: An exponential equation is one in which the variable to be solved for (call it x) is in an exponent. For example 3 x = 5 is an exponential equation while x 3 = 5 is not.Only certain types of exponential equations can be solved using algebra. We will study the following types. (Hover over the links to see examples.)
• The unknown, x, occurs only once. • The equation is of the form a · b x = c · d x. • The only exponential in the equation is b x, and it occurs several times. • The equation contains the exponentials b x, b 2 x, b 3 x, etc.
Exponential equations in which the unknown occurs just once
To solve this type of equation, follow these steps:- Identify the exponential.
- Invert the operations that were applied to the exponential in the reverse order in which they were applied.
The result is that the exponential stands alone on one side of the equation, which now has the form
b f = a, where the exponent f contains the unknown x.
- If the base of the exponential is e then
take natural logarithms of both sides of the equation.
Otherwise you may as well take logarithms in base 10. (Do not take logarithms in any
other base because your calculator cannot evaluate them.)
Immediately use property 3 of logarithms
to “bring down” the exponent. This puts the equation into one of these forms:
f · ln (b) = ln (a) or f · log (b) = log (a).
- In either case exponents are no longer involved. Finish solving for the unknown, x,
by using the basic steps for solving equations.
- Check the solution.
Example: Solve the exponential equation 2 · 5 x + 3 = 21 for x.
Solution: This equation contains a single exponential, 5 x. (Notice that the number 2 is not part of it!) To isolate the exponential, subtract 3 and then divide by 2 on both sides of the equation. The result is that the exponential is isolated on the left-hand-side of the equation:
5 x = 9.Take logarithms to base 10 of both sides:
log(5 x) = log(9)Use property 3 of logarithms to bring down the exponent:
x · log(5) = log(9)Solve for x:
Exponential equations of the form a · b x = c · d x
To solve this type of equation, follow these steps:- Make sure that the equation is of precisely the form
a · b x = c · d x.
There can only be two terms and one must be on each side of the equation.
- If the base of either exponential is e then
take natural logarithms of both sides of the equation.
Otherwise you may as well take logarithms in base 10. (Do not take logarithms in any
other base because your calculator cannot evaluate them.)
Immediately use property 3 of logarithms
to “bring down” the exponent on both sides of the equation. This puts the equation into one of these forms:
ln (a) + x · ln (b) = ln (c) + x · ln (d) or log (a) + x · log (b) = log (c) + x · log (d).
- In either case this is now a linear equation in x.
It is solved by collecting x terms on the left-hand-side and
factoring out x and collecting constant terms on the right:
x (log (b) − log (d)) = log (c) − log (a)
and then isolating x: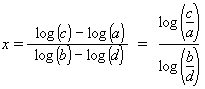
- Check the solution.
Example: Solve the exponential equation 5 · e 1.7 x = 2 · 4 2.9 x for x.
Solution: Because one of the exponentials has base e, take natural logarithms of both sides of the equation:
ln (5 · e 1.7 x ) = ln (2 · 4 2.9 x ).On both sides of the equation, use property 1 of logarithms to split up the logarithm of the product
ln (5) + ln (e 1.7 x ) = ln (2) + ln (4 2.9 x ).On the right-hand-side, use property 3 of logarithms to bring down the exponent. On the left-hand-side you could do the same, but instead you can just use the fact that the natural log and the exponential function cancel. This gives:
ln (5) + 1.7 x = ln (2) + 2.9 x ln (4)Simplify:
1.609 + 1.7 x = 0.6931 + 4.02 xThis is a linear equation in x. Solve it by collecting x terms on the left-hand-side and constant terms on the right, and then isolating x. The solution is x = 0.3949. Check this solution by substituting it into the original equation. This gives 9.784 = 9.784 so it checks out.
Exponential equations in which the same exponential occurs several times
To solve this type of equation, follow these steps:- Identify the exponentials in the equation and make sure that they are all identical.
Suppose that they are all equal to b f, where the exponent
f is an expression containing the unknown, x.
- Use an alias. Replace each occurrence of
b f with, say Q. This may turn the equation into a
linear or fractional or some other non-exponential type of equation in the variable Q.
Solve this equation for Q using the
usual techniques.
Then substitute back b f for Q.
At this point the equation has the form
b f = a, where the exponent f contains the unknown x.
- If the base is e then
take natural logarithms of both sides of the equation.
Otherwise you may as well take logarithms in base 10.
(Do not take logarithms in any other base because your calculator cannot evaluate them.)
Immediately use property 3 of logarithms
to “bring down” the exponent. This puts the equation either into one of these two forms:
f · ln (b) = ln (a) or f · log (b) = log (a).
- In either case exponents are no longer involved. Finish solving for the unknown x
by using the usual techniques.
- Check the solution.
Example: Solve this exponential equation for t:
Solution: This equation contains two identical exponentials, e−k t. We replace both occurrences of e−k t with Q:
This is now a fractional equation in Q. In order to clear the denominators, multiply both sides by 1 − Q:
a (1 − Q) = b (1 + Q).This is now a linear equation in Q. In order to collect like terms, distribute on both sides:
a − a Q = b + b Q.Collect the constant terms on the left-hand-side. Then collect the terms containing Q on the right-hand-side and factor out Q:
a − b = Q (a + b).Solve for Q:
Now substitute back e−k t for Q. The result is a single exponential that is isolated:
We are finally at the point where we can take natural logarithms. Doing so gives:
The unknown, t is no longer in the exponent. Now divide through by −k to solve to t:
We could leave the answer in this form or we could get fancy and use the fact that
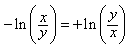 to get rid of a − sign and write the answer as:
to get rid of a − sign and write the answer as:
Exponential equations containing exponentials b x, b 2 x, b 3 x, …
Suppose that an exponential equation contains the exponentials b x, b 2 x, b 3 x, etc., where b could be any base. This type of equation can be solved by a slight extension of the alias method used above. It depends on the following observation:If b x is replaced by the alias, Q, thenThus all the exponentials can be replaced with positive integer powers of Q. Even exponentials like b 2 x + 1 can be expressed in terms of an integer power of Q since
b 2 x = (b x ) 2 = Q 2,
b 3 x = (b x ) 3 = Q 3,
b 4 x = (b x ) 4 = Q 4, etc.
b 2 x + 1 = b 1 · b 2 x = b Q 2Here are the steps to solve this type of equation:
- Identify the exponentials in the equation and make sure that naming one of them
Q makes all the others become positive integer powers of Q.
(This may well be the hardest step!)
- Use the alias.
Let b x be Q and express all the other exponentials
in terms of Q as well. This hopefully turns the equation into a
quadratic or polynomial or some other non-exponential type of equation in the variable Q.
Solve this equation for Q using the techniques for that type of equation.
Then substitute back b x for Q.
At this point the equation (or equations) have the form
b x = a.
- If the base is e then
take natural logarithms of both sides of the equation.
Otherwise you may as well take logarithms in base 10.
(Do not take logarithms in any other base because your calculator cannot evaluate them.)
Immediately use property 3 of logarithms
to “bring down” the exponent. This puts the equation either into one of these two forms:
x · ln (b) = ln (a) or x · log (b) = log (a).
- In either case exponents are no longer involved. Finish solving for the unknown x
by using the usual techniques.
- Check the solution.
Example: Solve the exponential equation e − 2 t + e − t + 1 − 1 = 0.
Solution: This is a quadratic equation in e − t as can be easily seen if we use the properties of exponents to rewrite it as:
(e − t ) 2 + e 1 · e − t − 1 = 0.Now replace e − t with the alias Q. The result is:
Q 2 + e Q − 1 = 0.(Recall that e is the number approximately equal to 2.718.) Solve this quadratic equation for x using the quadratic formula with a = 1, b = e and c = −1:
Now substitute back e − t for Q:
Since we can’t take the logarithm of a negative number the second solution is extraneous. That leaves the only solution:
t = −ln (0.3282) = 1.11
Note that not all exponential equations can be solved using algebra. For example consider the seemingly simple equation x = 10x. We cannot get the x out of the exponent without putting the other x into a logarithm. This equation can only be solved approximately using a computer.
12.7 - Logarithmic Equations
Before reading this section you may want to review the following topics: A logarithmic equation is one where the variable to be solved for (call it x) is in the argument of a logarithm function. For example log(x) = 5 is a logarithmic equation while log(5) = x is not. To solve a logarithmic equation follow these steps:- If the equation contains several logarithms then you must first use the
properties of logarithms
to combine them into a single logarithm.
- Isolate the logarithm. This means put the equation into the form
log b( f ) = a so that the log
function is alone on one side of the equation. (The expression
f contains the unknown x.)
- Antilog both sides, thus putting the
equation into the exponential form b a = f.
- The unknown x is no longer inside a logarithm.
Now you can finish solving for x
by using the basic procedures for solving equations.
- Check the solution.
Example: Solve the logarithmic equation 2 log 3 (x − 1) = 4 for x.
Solution: There is only a single logarithm so the first step is to isolate the logarithm. To do this divide both sides by 2:
log 3 (x − 1) = 2The next step is to antilog both sides:
x − 1 = 3 2The equation is no longer logarithmic and we can finish solving for x by simply adding 1 to both sides:
x = 10
Example: Solve the logarithmic equation log (3 x + 1) − 2 log (x) = 1 for x:
Solution: The first step is to combine the logarithms using the properties of logarithms. First use property 3, then property 2:
log(3 x + 1) − log (x2 ) = 1The next step is to antilog both sides. Note that the base of the logarithm is understood to be 10.
The equation is no longer logarithmic - it is fractional, so we can proceed to solve for x using techniques for fractional equations. Clear the denominator by multiplying through by x2 and then move all terms to the left side:
10 x 2 − 3 x − 1 = 0The result is a quadratic equation in standard form. The left-hand-side can be factored:
(5 x + 1) (2 x − 1) = 0.We can replace this equation by two new equations, each of which results from setting one of the factors equal to zero. Solving them yields the solutions:
Now we must check the solutions. Substituting x = 1/2 into the original equation and simplifying yields the equation 1 = 1, so it checks out. But substituting x = −1/5 into the original equation means that we must evaluate the logarithm of a negative number and this cannot be done over the real numbers. Thus this solution is extraneous; which leaves us with the only solution, x = 1/2.
Note that not all logarithmic equations can be solved using algebra. For example consider the seemingly simple equation x = log (x). We cannot get the x out of the logarithm without putting the other x into an exponential. This equation can only be solved approximately using a computer.