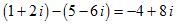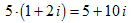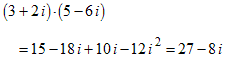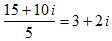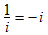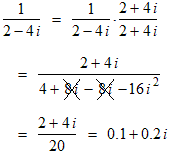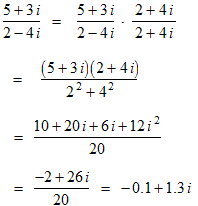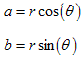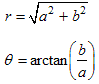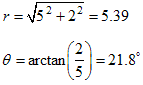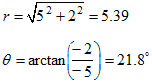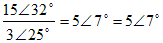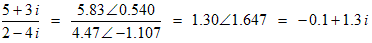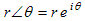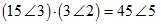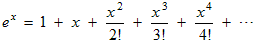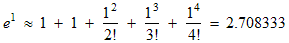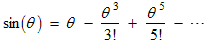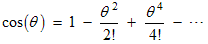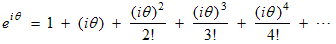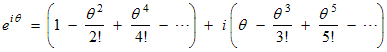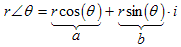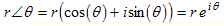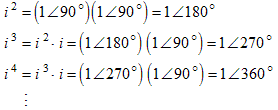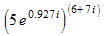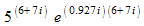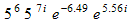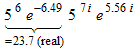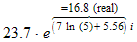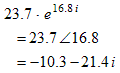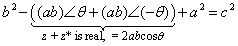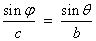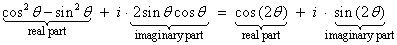Chapter 15 - Complex Numbers
The complex numbers are important for several reasons. First, the real numbers are incomplete. Many mathematical expressions such as arcsin (2), ln (−1) and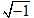 have no meaning over the real numbers and
many polynomials cannot be factored over the real numbers.
But if we include complex numbers in our number system then these expressions
all have values and every polynomial can be factored.
The complex numbers complete the number system.
have no meaning over the real numbers and
many polynomials cannot be factored over the real numbers.
But if we include complex numbers in our number system then these expressions
all have values and every polynomial can be factored.
The complex numbers complete the number system. Second, many real number problems have real solutions which cannot be found by using real arithmetic but can be found easily via complex arithmetic. The reason is that complex numbers add another dimension to the number system, thus opening up other routes to the solution.
Finally complex numbers lead to remarkable insights. For example complex numbers show that there is a very close connection between sinusoidal oscillations and exponential decay in a physical system.
This chapter contains the following sections:
- section 15.1 - In this section we introduce
complex numbers in rectangular form; how to add, subtract, multiply and divide them,
and how to graph them in the complex plane.
- section 15.2 - In this section we talk about complex numbers in polar form and exponential form and how to do arithmetic with them.
15.1 - Introduction to Complex Numbers
Note: Mathematicians use the expression “… over the complex numbers” to mean that the number system under consideration is the complex numbers, and the expression “… over the real numbers” to mean that the number system under consideration is the real numbers. For example they will say that the equation x 2 = −9 cannot be solved for x over the real numbers but that it has a solution over the complex numbers. |
Imaginary Numbers
First we introduce the imaginary numbers.
An imaginary number is the square root of a negative number.
The imaginary unit i is defined as:
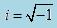
|
Note: Electrical engineering is one application that makes extensive use of complex numbers. Unfortunately the letter i is already used to represent electric current. Therefore electrical engineers usually use the letter j to represent the imaginary unit. The Algebra Coach has an option that allows you to set either i or j to represent the imaginary unit.
Here are some examples of arithmetic with imaginary numbers. The first example shows how the square root of any negative number can be expressed as a multiple of the imaginary unit i. The second example shows that squaring an imaginary number gives a negative number. The last example shows how any power of i can be simplified.
Complex Numbers
A complex number z is the sum of a real number plus an imaginary number. It can be written in the form:z = a + b iwhere a and b are both real numbers. a is called the real part of z and b is called the imaginary part of z. We write this as a = Re(z) and b = Im(z).
Example: If z = − 5 − 7 i then Re(z) = −5 and Im(z) = −7.
The complex conjugate of any complex number a + b i is defined to be a − b i. (The imaginary part just has its sign reversed.) The complex conjugate of z is denoted z*. For example if z = − 5 − 7 i then z* = − 5 + 7 i.
Arithmetic with Complex Numbers
We demand that imaginary numbers and complex numbers have all the properties that real numbers have, plus a few new ones that we will discover along the way. Here are some examples of arithmetic with complex numbers:
Graphing Complex NumbersComplex numbers can be displayed as points or arrows on the complex plane. The real part of the complex number is plotted along the real (horizontal) axis and the imaginary part is plotted along the imaginary (vertical) axis. Real numbers lie on the real axis and imaginary numbers lie on the imaginary axis.Complex numbers are similar to 2-dimensional vectors in the way they are added: you add horizontal components and you add vertical components. But complex numbers can also be multiplied whereas vectors can't. |
 |
15.2 - Complex Numbers in Polar and Exponential Form
Polar Coordinate FormThe form a + b i used so far for complex numbers is called the rectangular coordinate form of a complex number because to plot the number we imagine a rectangle of width a and height b, as shown in the graph above.But complex numbers, just like vectors, can also be expressed in polar coordinate form, r ∠ θ . (This is spoken as “r at angle θ ”.) The figure to the right shows an example. The number r in front of the angle symbol is called the magnitude of the complex number and is the distance of the complex number from the origin. The angle θ after the angle symbol is the direction of the complex number from the origin measured counterclockwise from the positive part of the real axis. For any complex number z, writing | z | denotes its magnitude. For example the four complex numbers 5 and −5 and 3 + 4 i and 5 ∠ 120° all have magnitude 5 because they are all a distance 5 from the origin. Using magnitude notation we write | 5 | = 5 and | −5 | = 5 and | 3 + 4 i | = 5 and | 5 ∠ 120° | = 5. |
 |
Polar → Rectangular ConversionSuppose we have a complex number expressed in polar form and we want to express it in rectangular form. (That is, we know r and θ and we need a and b.) Referring to the figure we see that we can use the formulas:Rectangular → Polar ConversionOn the other hand, suppose we have a complex number expressed in rectangular form and we want to express it in polar form. (That is, we know a and b and we need r and θ.) We see that we can use the formulas: |
 |
Example: Convert the complex number 5 ∠ 53° to rectangular form.
Solution: We have r = 5 and θ = 53°. We compute a = 5 cos (53°) = 3 and b = 5 sin (53°) = 4, so the complex number in rectangular form must be 3 + 4 i.
Example: Convert the complex number 5 + 2 i to polar form.
Solution: We have a = 5 and b = 2. We compute
so the complex number in polar form must be 5.39 ∠ 21.8°.
Example: Convert the complex number −5 − 2 i to polar form.
Solution: We have a = −5 and b = −2. We compute
which is exactly the same answer as for the previous example! That can't be. What went wrong? The answer is that the arctan function always returns an angle in the first or fourth quadrants and we need an angle in the third quadrant. So we must add 180° to the angle by hand. Thus the complex number in polar form must be 5.39 ∠ 201.8°.
Multiplying and Dividing Complex Numbers in Polar Form
Complex numbers in polar form are especially easy to multiply and divide. The rules are:- Multiplication rule: To form the product multiply the
magnitudes and add the angles.
- Division rule: To form the quotient divide the magnitudes and subtract the angles.
Example: multiply (5 ∠ 30°) · (3 ∠ 25°)
(5 ∠ 30°) · (3 ∠ 25°) = (5·3) ∠ (30+25)° = 15 ∠ 55°
Example: divide 15 ∠ 32° by 3 ∠ 25°
Example: divide 5 + 3 i by 2 − 4 i
Just for fun we converted both numbers to polar form (with angles in radians), then did the division in polar, then converted the result back to rectangular form.
Complex Numbers in Exponential Form
These rules about adding or subtracting angles when multiplying or dividing complex numbers in polar form probably remind you of the rules for adding or subtracting exponents when multiplying or dividing exponentials:x m · x n = x m + n and x m / x n = x m − n.They suggest that perhaps the angles are some kind of exponents. This guess turns out to be correct. We will prove in the next section that:
where as usual the base e is the number e = 2.71828… The form r e i θ is called exponential form of a complex number. The next example shows the same complex numbers being multiplied in both forms:
Notice that in the exponential form we need nothing but the familiar properties of exponents to obtain the result of the multiplication. That is much more pleasing than the polar form where we have to introduce strange rules about multiplying lengths and adding angles.
polar form exponential form
Proof that r ∠ θ = r e i θ
The proof that the polar and exponential forms of a complex number are equivalent, namely that r ∠ θ = r e i θ, requires the use of Euler’s formula, so we will first state and prove Euler’s formula. This formula states that:It is due to Leonard Euler and it shows that there is a deep connection between exponential growth and sinusoidal oscillations. To prove it we need a way to calculate the sine, cosine and exponential of any value of θ just like a calculator does. Taylor series provides a way.
e i θ = cos ( θ ) + i sin ( θ ) Euler’s formula
The Taylor series for e x is:
The notation 4! means 4 · 3 · 2 · 1, etc. The dots … indicate that the series (sum) goes on forever. The idea is that if we keep only the first few terms then we get an approximation for e x. The more terms we keep the better the approximation. If we could keep all the terms then we would get the exact answer. For example e 1 or e approximated by just the first 5 terms is already good to about 3 significant figures:
There are similar Taylor series for sin(θ) and cos(θ) :
and
(Important Note: these two formulas for the sine and cosine assume that θ is measured in radians. Measuring θ in degrees would not make sense because then each term in the series would have different units and then they couldn’t be added.) To prove Euler’s formula we will manipulate the left side until it becomes equal to the right side. First substitute the series for e x into the left side of Euler’s formula, replacing x by i θ :
Now simplify and group all the real terms together and group all the imaginary terms together. We get:
Now notice that the terms in the first brackets are just the Taylor series for cos(θ) and that the terms in the second brackets are just the Taylor series for sin(θ). Thus we have converted the left side of Euler’s formula to read cos(θ) + i sin(θ) which equals the right side of Euler’s formula. This ends the proof of Euler’s formula.
Now that we have Euler’s formula it is easy to prove that r ∠ θ = r e i θ. Again we will manipulate the left side until it equals the right side. First, convert the left side to rectangular form:
Now factor out r and use Euler’s formula on the terms in the brackets.
The result is that we have converted the left side to equal the right side. This proves that r ∠ θ = r e i θ
Examples Using Rectangular, Polar and Exponential Form
When doing calculations with complex numbers which form should you use? Generally speaking use rectangular form for adding and subtracting, polar form for multiplying and dividing, and exponential form for exponentiating or manipulating literal expressions. Here are some examples.Example 1: Show that e i π = −1. This is known as Euler’s identity.
Solution: Simply convert to polar and then to rectangular:
Example 2: Calculate i n for n = 1, 2, 3, …, plot the numbers on the complex plane, and spot the pattern.
Solution: The pattern is easiest to spot in polar,
where i = 1 ∠ 90°. Then:The plot is shown to the right. The various powers give a sequence of complex numbers that goes in a counterclockwise circle of radius 1 about the origin. After the 4th power the angle is greater than 360° but the counterclockwise pattern continues with new numbers falling on top of old numbers. |
 |
Example 3: Evaluate the exponential (3 + 4 i) (6 + 7 i)
Solution: Do the following manipulations:
Convert the base to exponential form. Remember the angle must be in radians. The base now contains two factors. Apply the property of exponents
(a b) m = a m · b m.Apply the property of exponents
b m + n = b m · b n.Move the real factors to the front and evaluate them. Change the base from 5 to e by using the identity
5 = e ln(5).Combine the exponents and evaluate. Express the answer in exponential, polar or rectangular form.
Many trigonometric laws and identities are easy to prove with complex numbers expressed in polar form. Among them are the sine and cosine laws, the sum of angles trigonometric identities, and De Moivre’s formula.
Proof of the sine and cosine laws
This proof uses the complex conjugate, denoted z*.
Recall that if z = a + b i is a complex number expressed in rectangular coordinates then z* = a – b i.
If z = r∠θ is a complex number expressed in polar coordinates then z* = r∠(−θ )
In general, to get the complex conjugate of any complex expression just change every i in the expression to –i and change every angle θ to –θ. The complex conjugate is useful because:
z + z* = 2 a = 2 r cos θ, which is always real,
z – z* =2 b i = 2 r i sin θ, which is always imaginary, and
z · z* = a2 + b2 = r2, which is always real and positive.

The figure to the right shows three complex numbers (the red arrows) satisfying the relationship
b∠θ − a∠0 = c∠φNotice that a, b and c are also the lengths of the sides of the gray triangle. Each number has a complex conjugate (the gray arrows). (a∠0, being real, is its own complex conjugate.) The complex conjugates obey the relationship
b∠(−θ) − a∠0 = c∠(−φ)If we multiply these two equations, expand and simplify, the cosine law pops out. First multiply the equations.
(b∠θ − a∠0) · (b∠(−θ ) − a∠0) = c∠φ · c∠(−φ)Now expand the LHS.
b2∠0 − ab∠θ − ab∠(−θ ) + a2∠0 = c2∠0Now simplify.
This is the cosine law, c 2 = a2 + b2 − 2 a b cos θ.
To prove the sine law just take the imaginary part of b∠θ − a∠0 = c∠φ. This gives b sin θ − 0 = c sin φ orwhich is the sine law.
Proof of the sum-of-angles identity sin(θ + φ) = sin(θ)·cos(φ) + cos(θ)·sin(φ).
Start with the multiplication rule in the form (1∠θ) · (1∠φ) = 1∠(θ + φ). Convert each complex number to rectangular using trigonometry. (That is, use r∠α = r cos α + i r sin α).(cos θ + i sin θ ) · (cos φ + i sin φ) = cos (θ + φ) + i sin (θ + φ)
Expand the LHS and simplify.
Equating imaginary parts gives the sum-of-angles identity for sine. Equating real parts gives the sum-of-angles identity for cos.
De Moivre’s formula
De Moivre’s formula states that(1∠θ )n = 1∠( n θ )where n is any integer. It can be generalized to read (r∠θ )n = r n∠( n θ ). To prove it just multiply the number r∠θ by itself repeated and simplify. For example
(2∠40°)3 = (2∠40°) (2∠40°) (2∠40°) = (2)3∠(40° + 40° + 40°) = 8∠120°
One application of De Moivre’s formula is to prove the double, triple and higher multiple-angle identities. For example start with (1∠θ ) · (1∠θ ) = 1∠(2 θ ) and convert to rectangular.
(cos θ + i sin θ ) · (cos θ + i sin θ ) = cos (2 θ ) + i sin (2 θ )
Expand the LHS and simplify.
Equating imaginary parts gives the double-angle identity for sin and equating real parts gives the double-angle identity for cosine.
DeMoivre’s formula can also be used to find the nth roots of any complex number r∠θ (more precisely, it can be used to solve the equation zn = r∠θ, where n is a positive integer, for z). There are n roots in all. One root (called the principal root) can be found by taking the nth root of the length and one-nth of the angle. Thus it is r 1/n∠(θ /n). The other n – 1 roots are distributed uniformly in a circle about the origin in the complex plane. This uniform distribution guarantees that they all produce the same nth power.
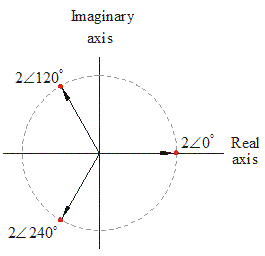
For example let’s find the cube roots of 8 (i.e. let’s solve the equation z3 = 8 for z). Write 8 as 8∠0°. The principal cube root is 81/3∠(0°/3) or 2∠0° or 2. Now distribute the three roots uniformly in a circle about the origin as illustrated by the red dots in the figure. We can verify that they are cube roots of 8 by cubing them using De Moivre’s theorem:
(2∠0°)3 = 8∠0° = 8
(2∠120°)3 = 8∠360° = 8
(2∠240°)3 = 8∠720° = 8