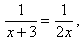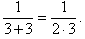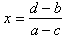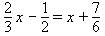Chapter 4 - Equations
Equations express relationships among quantities. They are statements of mathematical facts or of physical laws.
In geometry, for example, we can write down the equation A = π r 2, which relates the area A of a circle to its radius r. This equation is a mathematical fact. In physics we can write down the equation F = m a, which relates the amount of acceleration a that an object with mass m undergoes when a force F is applied to it. This equation is a law of nature called Newton’s second law of motion.If we are given a value for the radius of a circle then we can substitute it into the equation A = π r 2 and immediately get out the area of the circle. However if we are given the area and want to find the radius then we have to solve the equation for the radius.
This chapter and much of this book is concerned with solving equations. This chapter contains the following sections:
- Section 4.1 - In this section we introduce equations and their solutions. Then we talk about two types of equations that are easy to solve:
- Section 4.2 - In this section we show how to
solve the simplest equations in which the unknown appears more than once, namely
linear equations. Specifically we talk about these techniques:
Then we present a flowchart for solving equations.
In later chapters we will learn more specialized procedures for solving more specialized
equation types and will add to this flowchart.
- Section 4.3 - In this section we talk about extraneous solutions and how to deal with them, and lost solutions and how to avoid them.
4.1 - Introduction to equations
Definition: An equation is an algebraic statement that two expressions are equal. An equation consists of:
|
Here are three examples:
- 5 + 3 = 8
- 5 + 3 = 9
- x + 4 = 10
Solutions
Finding all the values of the variable x that make the left-hand-side of an equation equal the right-hand-side is called solving the equation for x. When we set out to find these values, x is called the unknown. Once we have found the values they are called the solutions or roots of the equation. We say that they make the equation true. We also say that these values of x satisfy the equation.Equations can have any number of solutions, as these examples show.
Example: The equation:
has one solution, namely x = 3. We can verify that this solution satisfies the equation by substituting it back into the equation. This gives:
Since both the left-hand-side and the right-hand-side simplify to 1/6, the solution x = 3 is verified.
Example: The equation:
20 x 3 + 25 x 2 + 5 x = 0has three solutions: x = 0, x = −¼ and x = −1. This is called a solution set. We can verify that all three values of x satisfy the equation by substituting each of them into the equation and getting the true statement that 0 = 0.
Example: Some equations have no solutions over the real numbers but do have solutions over the complex numbers. An example is the equation:
x 2 = −9.There is no real number which when squared will yield −9 but there are two complex numbers, namely 3 i and −3 i.
Example: Some equations have no solutions whatsoever. They are called contradictions. An example is the equation:
x = x + 1.There is no number that is unchanged when you add 1 to it.
Checking the solutions
Once you have found a possible solution for an equation you must substitute it into the original equation and check that it does indeed satisfy the equation. The reason is that the algebra process that we will describe below for solving an equation can produce so-called “extraneous solutions” (essentially garbage solutions!) You can’t tell that you have an extraneous solution until you substitute the solution in and discover that it doesn’t satisfy the original equation. Extraneous solutions must be rejected. Click here to learn more about extraneous solutions.Literal equations and formulas
Many of the equations that we will study will contain only numbers and one letter, namely the variable that is the unknown to be solved for. This letter will usually be x, the universal letter that represents the “unknown” (think x-rays, The x-Files, etc.) But we will also learn how to solve literal equations and formulas:- Literal equations are equations that contain more than one letter.
An example is a x + b = 10. One letter, usually x,
is considered to be the variable or unknown to be solved for
and the other letters are considered to be constants.
- Formulas are equations that also contain more than one letter. The letters are chosen to suggest certain physical quantities and any one of them can be considered to be the unknown. An example is the formula A = ½ b h, which gives the area A of a triangle having base b and height h.
- Don’t forget to set the AutoSolve unknown to whatever the
equation’s unknown is (by using either the Tools, Options menu or by clicking
on the status panel at the bottom of the program).
By default it is x.
- If the equation contains only numbers and one letter (the unknown) then the solution will be
a number and the Algebra Coach will check the solution. However if the equation
is a literal equation or formula then the solution will contain letters and the
Algebra Coach will not check the solution.
Basic procedures for solving equations
There is one basic rule to follow when solving equations:Perform the same mathematical operation on both sides of the equation. |
The reason is that this maintains the equality of the equation. The only question now is “which operation”? As we go through this book we will answer that question for ever more complicated types of equations. We begin, in this section, by explaining how to solve two of the simplest types of equations:
- equations in which the unknown occurs only once, and
- equations of the form a · b = 0.
After that we will manipulate every equation we encounter, no matter how complicated, until we get it into one of these two forms.
Solving equations in which the unknown occurs only once
Let’s assume that the unknown is x. The goal is to get x alone on one side of the equation. To do this, look at what operations have been applied to x to get the expression that contains x. Then:Invert (undo) the operations that were applied to x in the reverse order in which they were applied. |
Every operation that is performed on the left-hand-side of the equation is also performed on the right-hand-side. Also, after every algebraic operation, both sides are simplified as much as possible.
Example: Solve the equation:
x − 5 = 13.Solution: In the expression on the left-hand-side of the equation, x has had 5 subtracted from it so we must add 5 back on to get x alone. (Adding 5 is the inverse operation of subtracting 5.) Adding 5 to both sides gives:
x − 5 + 5 = 13 + 5.Simplifying both sides then gives:
x = 18.This last equation is just a manipulated form of the original equation, but because it has x alone on the left-hand-side and a number on the right-hand-side, it is the solution. We must still check the solution by substituting it into the original equation. This gives 18 − 5 = 13 or 13 = 13, so the left-hand-side equals the right-hand-side and the solution checks out.
Example: Solve the equation:
Solution: In the expression on the left-hand-side of the equation, x has had this sequence of operations applied to it in this order:
- subtraction of 8
- square root
- multiplication by 2
- division by 2 (this is the inverse of the multiplication by 2)
- square (this is the inverse of the square root)
- addition of 8 (this is the inverse of the subtraction of 8)
Why these operations and why this order? Here is an analogy. Picture how you get dressed in the morning (to be polite we will only talk about socks and shoes):
Also note that since your shoes were put on last they have to come off first. |
Therefore start with
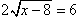 and perform this sequence of
operations:
and perform this sequence of
operations:
- Divide both sides by 2 and simplify:
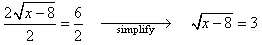
- Square both sides and simplify (note that on the left-hand-side the
square and square root are inverse operations):
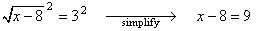
- Add 8 to both sides and simplify:
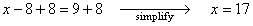
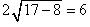 which simplifies to 6 = 6,
so the left-hand-side equals the right-hand-side and the solution checks out.
which simplifies to 6 = 6,
so the left-hand-side equals the right-hand-side and the solution checks out.
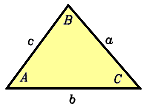 Example: The cosine law,
Example: The cosine law,
is a formula that is used to solve oblique triangles. It is a relation between the lengths of sides a, b and c and the angle C which is opposite side c. Given any three of these quantities, the fourth can be found. Solve the cosine law for angle C.,
Solution: On the left-hand-side the variable C has had these operations applied to it in this order:
- application of the cosine function
- multiplication by −2 · a · b
- the addition of a 2 + b 2
- the subtraction of a 2 + b 2
- division by −2 · a · b
- application of the arccos function (this is the inverse of the cosine function)
Therefore start with
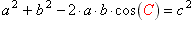 and perform this sequence of
operations:
and perform this sequence of
operations:
- Subtract a 2 + b 2 from both sides and simplify:
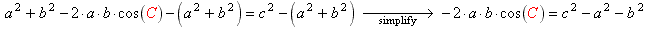
- Divide both sides by −2 · a · b and simplify:

- Apply the arccos function to both sides and simplify (note that
cos and arccos are inverse functions):
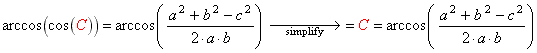
Solving equations of the form a · b = 0
Suppose that a and b are any expressions. Then the following statement is true: If a · b = 0 then either a = 0, or b = 0, or both.In other words a product can equal zero only if one of its factors is zero. This fact can be used to replace a “complicated” equation a · b = 0 by two simpler equations a = 0 and b = 0. |
Note:
- It must be a product on the left-hand-side. Addition, subtraction or division will not work.
For example a + b = 0 does not imply that
a or b have any particular values.
- It must be zero on the right-hand-side. Any non-zero number will not work. For example a · b = 6 does not imply that a or b have any particular values.
Example: Solve the following equation for x:
(x − 1)(x + 2) = 0.Solution: There are two factors on the left-hand-side of the equation:
- x − 1, and
- x + 2.
- x − 1 = 0, and
- x + 2 = 0.
- x = 1
- x = −2
- Substitute 1 in for x in the original equation. This gives (1 − 1)(1 + 2) = 0,
which simplifies to 0 = 0 so this solution checks out.
- Substitute −2 in for x in the original equation. This gives (−2 − 1)(−2 + 2) = 0,
which simplifies to 0 = 0 so this solution checks out.
Example: Solve the following equation for x:
5 x (x + 1)(4 x + 1) = 0.Solution: There are four factors on the left-hand-side of the equation:
- 5,
- x,
- x + 1, and
- 4 x + 1.
- 5 = 0,
- x = 0,
- x + 1 = 0, and
- 4 x + 1 = 0.
- this equation is a contradiction; it has no solution
- there is nothing to do - this equation is already solved; the solution is x = 0
- subtract 1 from both sides; this equation has the solution x = −1
- subtract 1, then divide by 4 on both sides; this equation has the solution x = −¼
Notes:
- Since the first factor, 5, obviously can’t equal zero you could simply
ignore it and consider only the other three factors.
- Another approach is to begin this problem by dividing both sides of the
original equation by 5. This gives the following equation in which
the factor of 5 doesn’t appear:
x (x + 1)(4 x + 1) = 0.
But note that you can’t divide by any of the other factors, say by x, because that would amount to dividing by zero, which is an undefined operation. (Also it would cause you to lose that corresponding solution.)
- In a previous example we looked at the equation
20 x 3 + 25 x 2 + 5 x = 0.
We didn’t solve it but we did verify that it has the same three solutions as the present example, namely x = 0, x = −1 and x = −¼, by substituting them back in and checking. In fact the only difference between that previous example and our present example is that left-hand-side of the equation in this present example is in factored form and in the previous example it is not. In fact, manipulating equations into the form a · b = 0 is one of the most important applications of factoring.
4.2 - Linear equations
A linear equation is an equation in which the terms containing the unknown are all of first degree. Assuming that the unknown is x, this means that the equation does not contain powers of x such as x 2 or x 3 or functions of x such as sin(x). A linear equation has the form:
a x + b = c x + d,where a, b, c and d are constants; or it can be put into this form by distributing. Any term containing x is called a linear term and any term not containing x is called a constant term. Here are some examples of linear equations:
- 1.6 (x + 2.2) = −1.7
- x = −4
- 5 x + 2 = −22 − x
- 3 (2 x + 1) = 9 (x − 4)
- ½ (x + ¼) = ¾ x
Technique 1: Collecting like terms
If there are like terms on one side of the equation then combine them. (All the linear terms in the equation are considered to be alike, and all the constant terms are considered to be alike.) Combining the linear terms turns an equation in which the unknown appears more than once into one in which the unknown appears only once, and we have already seen how to solve that type. |
Example: Solve this equation for x:
3 x + 5 x = −16.Solution: Combine the like terms on the left side of the equation:
8 x = −16.Notice that this gives an equation in which x appears just once. Now divide both sides by 8:
x = −2.This is the solution. Check it by substituting back into the original equation. This gives −16 = −16, so the solution checks out.
Suppose that there are like terms, but on opposite sides of the equation. Then choose one of the terms and subtract (or add) it to both sides of the equation. This makes that term disappear from one side of the equation and makes its opposite or negative appear on the other side of the equation. This is called “transposing the term”. Continue transposing terms until you have collected all the linear terms on one side of the equation and all the constant terms on the other side of the equation. With all the like terms now on the same side of the equation, they can be combined. |
Example: Solve this equation for x:
3 x + 22 = −5 x + 6.Solution: There are linear terms on both sides of the equation. Transpose the −5 x term to the left-hand-side by adding 5 x to both sides of the equation:
3 x + 22 + 5 x = −5 x + 6 + 5 xNotice how −5 x has disappeared from the right-hand-side and +5 x has appeared on the left-hand-side. There are constant terms on both sides of the equation so transpose the 22 term to the right-hand-side by subtracting 22 from both sides:8 x + 22 = 6.
8 x + 22 − 22 = 6 − 22Notice how +22 has disappeared from the left-hand-side and −22 has appeared on the right-hand-side.8 x = −16.
At this point the collecting of like terms is complete: All of the linear terms containing x have been collected on the left-hand-side of the equation and all the constant terms have been collected on the right-hand-side of the equation and x now appears just once. Divide both sides by 8 and we have the solution:
x = −2.Check it by substituting back into the original equation. This gives 16 = 16, so the solution checks out.
To collect like linear terms that have literal coefficients, simply factor x out of them. For example, to collect a x + b x − c x, factor like this: x (a + b − c). |
Example: Solve this literal equation for x:
a x + b = c x + d.Solution: We perform exactly the same steps as in the previous example. Transpose the c x term to the left-hand-side by subtracting c x from both sides of the equation:
a x + b − c x = c x + d − c xNow transpose the b term to the right-hand-side by subtracting b from both sides:a x − c x + b = d.
a x − c x + b − b = d − bIn the previous example we combined the x terms like this:a x − c x = d − b.
3 x + 5 x → (3 + 5) x → 8 x.The blue factoring step was not shown but it was implied. We do the same thing here to collect the x terms: we factor out the common factor of x on the left-hand-side. This puts the equation in the form:
x (a − c) = d − bAt this point the collecting of like terms is complete. All the terms containing x have been collected on the left-hand-side of the equation and all the constant terms have been collected on the right-hand-side of the equation and x now appears just once. Divide both sides by a − c and we have the solution:
Technique 2: Distributing
Suppose that a linear equation has a linear term and a constant term together in brackets. Then in order to collect linear terms on one side of the equation and constant terms on the other side, we must use the distributive law to remove the brackets. |
Example: Solve this equation for x:
2 (19 − 7 x) = 5 x.Solution: Because the 19 term and the 7 x term are together inside brackets there is no way to transpose one without the other. Therefore we must distribute on the left-hand-side. This gives:
38 − 14 x = 5 x.Now we can transpose the 14 x term to the right-hand-side by adding 14 x to both sides. This gives:
38 = 19 x.(Note that we could have transposed either the 14 x term to the right-hand-side or the 5 x term to the left-hand-side. We chose to transpose the 14 x term because (1) it results in one less algebra step to get the solution, and (2) it gives us a positive term, namely 19 x, on the right, rather than a negative term, −19 x, on the left.)
Now the unknown appears just once. Divide both sides by 19. This gives:
2 = x,which means that the solution is x = 2. Substituting the solution back into the original equation gives 10 = 10, so it checks out.
Note: Just because a linear equation has brackets does not necessarily mean that you should distribute. Here are two examples where you shouldn’t:
- a (x + b) = c
← don’t distribute; x occurs only once
- (a + b) x = c x + d ← don’t distribute; the brackets contain only constants
Technique 3: Clearing fractions, decimal coefficients and large coefficients
Equations are generally easier to solve if they don’t contain fractions or decimal coefficients or large coefficients. To clear an equation of fractions, carry out the following steps:
|
Example: Solve this equation for x:
Solution: First we will clear the fractions. Here are the required steps:
- The fractions have denominators of 3, 2 and 6. The LCM of these numbers is 6.
- Multiply both sides of the equation by 6. Don’t forget to put brackets
around both sides of the equation:
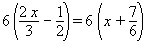
- Distribute on both sides of the equation:
4 x − 3 = 6 x + 7.
−2 x − 3 = 7.Add 3 to both sides. This gives:
−2 x = 10.Divide both sides by −2. This gives the solution:
x = −5.Check it by substituting it back into the original equation. This gives −23 / 6 = −23 / 6, so the solution checks out.
To clear an equation of decimals, carry out the following steps:
|
Example: Solve this equation for x:
7.2 x − 16 = 8.48Solution: First we will clear the decimals. Here are the required steps:
- The coefficients that have decimal points are 7.2 and 8.48.
Multiplying them by 100 will turn them both into integers.
- Multiply both sides of the equation by 100. Don’t forget to put brackets
around both sides of the equation:
100 (7.2 x − 16) = 100 (8.48)
- Distribute on both sides of the equation:
720 x − 1600 = 848.
720 x = 2448.Divide both sides by 720. This gives the solution:
x = 3.4.Note that generally if an equation contains decimals then you should give the solution in decimal form as well. Check the solution by substituting it back into the original equation. This gives 8.48 = 8.48, so the solution checks out.
To clear an equation of large coefficients, carry out the following steps:
|
Example: Solve this equation for x:
150 x = 100 x + 250.Solution: First we will clear the equation of large coefficients. Here are the steps:
- Identify the largest factor that can be factored out of both sides of the
equation. It is 50.
- Factor 50 out of both sides of the equation:
50 (3 x) = 50 (2 x + 5).
- Cancel (divide by) 50 on both sides of the equation:
3 x = 2 x + 5.
x = 5.Check the solution by substituting it back into the original equation. This gives 750 = 750, so the solution checks out.
A flowchart for solving simple equations
Here is a flowchart that shows the procedure for solving all of the basic types of equation that we have seen in this chapter. The red area at the top refers to equations of the type a · b = 0, the green area on the left refers to equations in which the unknown occurs just once, and the blue area on the right refers to linear equations. In later chapters we will encounter more complicated types of equations and then we will add new sections to this flowchart where the ??? circle is.To use the flowchart, start at the “Start” ellipse and follow the arrows until you reach the “equation solved, check solution” ellipse. At a diamond you are asked a question and you proceed in one of two directions depending on your answer. At a rectangle you perform some operation. Click on any diamond or rectangle to see details or an example.

4.3 - Extraneous and Lost Solutions
Extraneous solutions
Suppose that x is the variable to be solved for in some equation. If we increase the degree of x in the equation (for example, by multiplying through by x − a, clearing the denominator, cross-multiplying, squaring both sides of the equation, etc.) then we run the risk of introducing extraneous solutions. These are false solutions that are created in the algebra process but that do not satisfy the original equation.For example, the equation
x − 3 = 0obviously has one solution, x = 3. But, if (for some reason) we multiply both sides of the equation by x then we get the equation
x (x − 3) = 0,which has two solutions x = 0 and x = 3. The solution x = 0 does not satisfy the original equation and is therefore extraneous.
Often in the algebra process there is no way to avoid introducing extraneous solutions. The only recourse is to check all our solutions by substituting them back into the original equation. Any that don’t satisfy the original equation are extraneous and must be dropped.
Lost solutions
Suppose that x is the variable to be solved for in some equation. If we decrease the degree of x in the equation (for example by dividing through by x − a or by taking the square root of both sides of the equation) then we run the risk of losing solutions. But there is an easy way to avoid this problem. Never divide an equation through by any expression containing x that could equal zero. Instead simply keep the factors.For example, the equation
5 x (x − 1) (x 2 + 1) = 0can be simplified by dividing both sides by 5 and by x 2 + 1 since neither quantity can equal zero. Doing so gives us the equation
x (x − 1) = 0.But we can’t divide through by x or x − 1 because then we will lose the solutions x = 0 and x = 1.