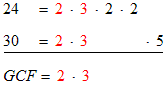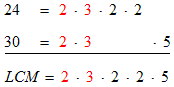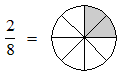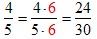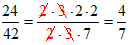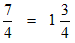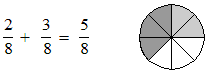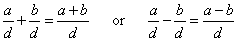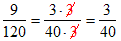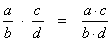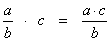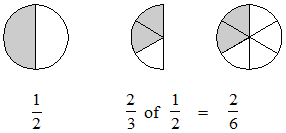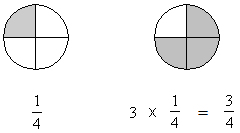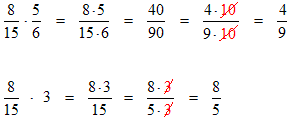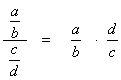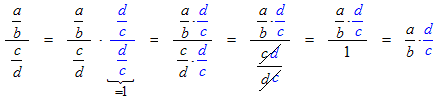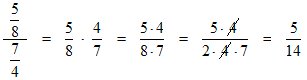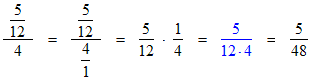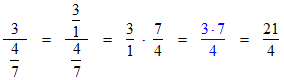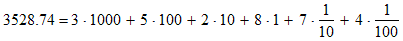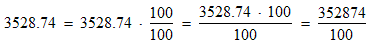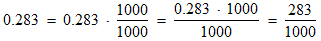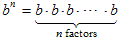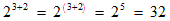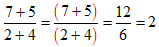Chapter 1 - Some Pre-Algebra Topics
1.1 - Factors of a number
The numbers that we are interested in factoring are the natural numbers 1, 2, 3, … The word factor is used as both a noun and a verb. The factors (noun) of a number are the numbers that divide evenly into the number. For example the factors of the number 12 are the numbers 1, 2, 3, 4, 6 and 12. (Notice that the smallest factor is always 1 and the biggest factor is always the number itself.)To factor (verb) a number means to express it as a product of smaller numbers. For example we can factor the number 12 like this: 12 = 3 · 4. The numbers 3 and 4 are called the factors. Another way to factor 12 is like this: 12 = 2 · 2 · 3. Now the factors are 2, 2 and 3. Each way of factoring a number is called a factorization.
A number that cannot be factored further is called a prime number. To factor a number completely means to write it as a product of prime numbers. This is also called the prime factorization.
Here are some examples of numbers in completely factored form:
100 = 2 · 2 · 5 · 5
18 = 2 · 3 · 3
29 = 29 (29 is a prime number)
Greatest Common Factor (GCF) of two numbers
If we look at two or more numbers then they will have factors in common. For examplethe factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40,We have shown the common factors in red. The greatest common factor is the largest of all the common factors. The greatest common factor of 40 and 50 is 10. Here are some more examples of greatest common factors:
and the factors of 50 are 1, 2, 5, 10, 25 and 50.
the GCF of 24 and 30 is 6
the GCF of 24, 30 and 33 is 3
the GCF of 7 and 21 is 7
the GCF of 7 and 13 is 1
Here is a procedure to find the greatest common factor of two or more numbers. We illustrate with the numbers 24 and 30. Factor the numbers completely and line up their factors. (By this we mean put common factors below each other and when either number is missing a factor then leave a space for it.)
Now it is easy to see the factors that both numbers have in common. Because they both have 2 and 3 in common the greatest common factor must be 2 · 3 = 6.
Lowest Common Multiple (LCM) of two numbers
The multiples of a number are the numbers that have that number as a factor. For example the multiples of 5 are 5, 10, 15, 20, 25, …If we look at two or more numbers then they will have multiples in common. For example
the multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, …We have shown the common multiples of 3 and 4 in red. They are 12, 24, … The smallest of the common multiples is called the lowest common multiple. Here are some more examples of lowest common multiples:
and the multiples of 4 are 4, 8, 12, 16, 20, 24, 28, …
the LCM of 9 and 20 is 180
the LCM of 2, 3 and 5 is 30
the LCM of 7 and 21 is 21
Here is a procedure to find the lowest common multiple of two or more numbers. We illustrate with the numbers 24 and 30. Factor the numbers completely and line up their factors. (By this we mean put common factors below each other and when either number is missing a factor then leave a space for it.)
The lowest common multiple must contain all the factors that are in either one number or the other, but the factors are not used twice when they are common to both numbers. Lined up like this it is easy to spot the common factors. The lowest common multiple must be 2 · 3 · 2 · 2 · 5 = 120.
You often need to find the factors that each of the original numbers must be multiplied by to give the LCM. Lined up like this they are easy to spot. They are just the missing factors. In this example 24 must be multiplied by the missing 5, and 30 must be multiplied by the missing 2 · 2 or 4.
1.2 - Fractions and how to add, subtract, multiply and divide them
Fraction notation
Fractions (or common fractions) are used to describe a part of a whole object. There are several notations for fractions:a is called the numerator and b is called the denominator. The notation means that we break an object into b equal pieces and we have a of those pieces. The portion or fraction of the object that we have is a/b. For example if we break a pie into 4 equal pieces and take 1 piece then we have 1/4 of the pie:
Equivalent fractions
Notice that we get the same amount of pie as in the previous example if we divide the pie into 8 equal pieces and get 2 of them:Fractions like 1/4 and 2/8 that have the same value are said to be equivalent fractions. This example suggests the following method for testing if two fractions are equivalent.
|
Two fractions are equivalent if multiplying the numerator and denominator of one fraction by the same whole number yields the other fraction. |
For example 4/5 and 24/30 are equivalent because we can start with 4/5 and multiply the numerator and denominator each by 6 to get 24/30:
Going in the opposite direction (from 24/30 to 4/5) suggests the following method for reducing a fraction to lowest terms or to its simplest equivalent fraction:
|
To reduce a fraction to lowest terms or to its simplest equivalent fraction, factor both the numerator and denominator completely (i.e. into prime numbers). Then cancel every factor that occurs in both the numerator and denominator. What remains is the simplest equivalent fraction. |
For example, here is how to reduce the fraction 24/42 is its simplest equivalent fraction, namely 4/7:
Improper fractions, mixed fractions and long division
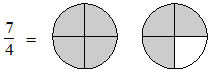
A fraction where the numerator is smaller than the denominator is called a proper fraction and a fraction where the numerator is bigger than the denominator is called an improper fraction. An example of an improper fraction is 7/4. Using the pie example this means that you have broken many pies each into 4 equal pieces and you have 7 of those pieces:Improper fractions are sometimes expressed in mixed fraction notation, which is the sum of a whole number and a proper fraction, but with the + sign omitted. For example 7/4 in mixed fraction notation looks like this:
Mixed fraction notation is not used in this Algebra Help e-book or in the Algebra Coach program because it is too easy to confuse it with the product of a whole number and a fraction. Instead of writing
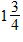 we will keep the + sign and write
we will keep the + sign and write 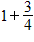 .
.
Long division is the method used to convert an improper fraction to a mixed fraction. We will illustrate the method on the fraction
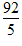 .
Carry out the following steps:
.
Carry out the following steps:
- Set up the long division format, namely
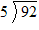 .
.
- Since 5 into 9 goes 1 time, write a “1” above the 9, write 1 × 5 or
“5” below the 9, and subtract 5 from 9 to get a difference of 4, like this:
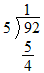
- Then bring down the 2 like this:
Here is what we have actually done: The “1” and “5” are in the tens place so they actually represent the numbers 10 and 50 as shown here: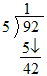
Therefore we have actually shown that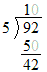
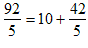 .
.
- Now repeat the entire process with the remainder, 42. Since 5 into 42 goes 8 times, write an “8” above the 2, write 8 × 5 or
“40” below the 42, and subtract 40 from 42 to get a remainder of 2, like this:
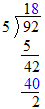
- This shows that that
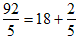 .
Since the remainder, 2, is smaller than the divisor, 5, this is our final
mixed fraction result.
.
Since the remainder, 2, is smaller than the divisor, 5, this is our final
mixed fraction result.
Some special fractions
There are several special fractions that are important to recognize: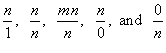
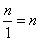 . Any number n can be turned into
a fraction by writing it over a denominator of 1.
. Any number n can be turned into
a fraction by writing it over a denominator of 1.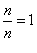 . Anything divided by itself equals 1.
We call this a UFOO (a useful form of one).
More on UFOOs later.
. Anything divided by itself equals 1.
We call this a UFOO (a useful form of one).
More on UFOOs later.- If the numerator of a fraction is a multiple of the denominator
then the fraction is equal to a whole number. An example is
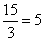 .
. 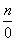 is undefined for any numerator n.
Division by zero is not allowed in mathematics.
is undefined for any numerator n.
Division by zero is not allowed in mathematics.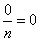 . A zero numerator is not a problem. This fraction equals 0.
. A zero numerator is not a problem. This fraction equals 0.
Adding or subtracting fractions
This picture shows that 2/8 of a pie plus 3/8 of a pie equals 5/8 of a pie:Fractions that have the same denominator are called like fractions. If you think about this example, then the following procedure for adding or subtracting like fractions is obvious:
|
To add two or subtract like fractions (fractions that have a common denominator), just add or subtract the numerators and put the result over the common denominator, like this: |
But what if the fractions don’t have a common denominator? The answer is that they must then be converted to equivalent fractions that do have a common denominator. The procedure is illustrated in this example:
The steps are:
- Find the lowest common multiple of the two
denominators 24 and 30. When applied to fractions this number is called the lowest common
denominator (LCD). In this example the LCD is 120.
- Convert each fraction to an equivalent fraction that has the
LCD of 120 as its denominator. To do this in this example multiply the numerator and
denominator of the first fraction by 5 and the numerator and denominator
of the second fraction by 4 (shown in red).
- Add the numerators and place over the common denominator.
Here are some more examples:
Multiplying fractions
Multiplying fractions produces a new fraction. Multiply the numerators to get the new numerator and multiply denominators to get the new denominator, like this: Then simplify by reducing the new fraction to lowest terms. To multiply a fraction by a whole number, just multiply the fraction’s numerator by the whole number to get the new numerator, like this: Then simplify by reducing the new fraction to lowest terms. |
Here is an example of why the first procedure works. Suppose that there is half a pie (the fraction 1/2) as shown on the left. Now suppose that you take 2/3 of that half pie. (The word “of” translates into the mathematical operation “multiply”.) This means that you cut the half pie into 3 equal pieces and take 2 of them. The result is 2/6 of the pie.
Here is an example of why the second procedure works. Suppose that you ate 1/4 of a pie and that your friend ate 3 times as much pie as you did. This means that your friend ate 3/4 of the pie.
Here are some more multiplication examples:
Reciprocals and dividing fractions
Reciprocals play an essential role when dividing fractions. Two numbers or fractions are said to be the reciprocals of each other if their product is 1. For example:4/5 and 5/4 are reciprocals because
8 and 1/8 are reciprocals because
Dividing fractions: The procedure is to replace a division by a fraction by the multiplication by the reciprocal of that fraction, like this: |
Notice that you take the reciprocal of the fraction on the bottom!
Here is why this procedure works: The key is that instead of seeing a fraction divided by a fraction, look for a single fraction whose numerator and denominator just happen to be fractions. In the first step we multiplied this fraction by a UFOO whose numerator and denominator just happen to be fractions. The UFOO was chosen so the fractions in the denominator would cancel and give 1. After another simplification that left only the final multiplication of fractions. |
Example 1: A fraction divided by a fraction:
Example 2: A fraction divided by a number. Notice that we have drawn one divide line longer than the other so you can tell which is the fraction and which is the number. The first step is to convert the whole number 4 into the fraction 4/1. After several steps you get the expression shown in blue. If you compare this expression to the original one you will notice a nice shortcut. The number 4 that you are dividing the fraction by simply becomes a new factor in the fraction’s denominator.
Example 3: A number divided by a fraction. Check the steps. This one is quite different from the previous example!
1.3 - Decimal notation
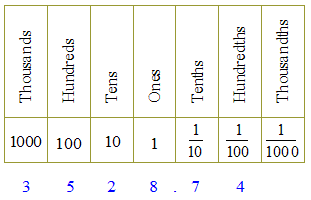
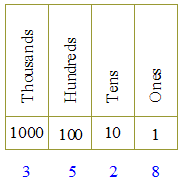
The word decimal means ten. The decimal number system is the familiar system that uses just ten symbols (numerals) to create any whole number, no matter how big. Those symbols are of course 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. (In contrast the binary number system uses just the two symbols 0 and 1 and the hexadecimal number system uses the sixteen symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F to create any number. Binary and hexadecimal are the number systems used in computers.)To create numbers bigger than 9 the decimal system uses place-values. For example the place-value chart on the right shows that 3528 means
|
3528 =
3 · 1000 + 5 · 100 +
2 · 10 + 8 · 1 This is because the 3 is in the thousands place, the 5 is in the hundreds place, the 2 is in the tens place and the 8 is in the ones place. Notice that as we move from right to left in the place-value table, the value of each place is ten times the value of the place to its right. |
|
If we continue this pattern to the right then we get the expanded place-value chart shown here:
A decimal point is used to separate the digit in the ones place from the digits to the right of it. The decimal number 3528.74 means:
Converting numbers from decimal to fraction notation:
We have seen before that whole numbers can be converted to fraction notation by simply putting them over 1.
Decimal numbers with digits to the right of the decimal point can be converted to fraction notation by multiplying them by a UFOO. First identify the place-value of the right-most digit. If the place-value is tenths then multiply by 10/10, if it is hundredths then multiply by 100/100, etc. Then simplify the numerator. This turns the numerator into a whole number. Here are some examples:
Exponential notation
Exponential notation is a convenient shorthand for repeated multiplication. The exponential b n means multiply b times itself n times:b is called the base, n is called the exponent, and we say that we are “raising b to the n th power” (except when n is 2 we say that we are “squaring b” and when n is 3 we say that we are “cubing b”).
Here are two examples:
3 4 = 3 · 3 · 3 · 3 = 81Important: To avoid confusion make sure you write the exponential neatly, with the exponent smaller and higher than the base. For example, did that person write the exponential 3 4 or just the number 34 ???
4 3 = 4 · 4 · 4 = 64
1.4 - Order of operations
An expression is a set of numbers that are combined using operations such as addition, subtraction, multiplication, division, exponentiation, etc. An example of an expression is:4 + 5 · 2 3.In this expression the numbers are 4, 5, 2 and 3 and they are combined by the operations of addition, multiplication and exponentiation.
Expressions often use brackets ( ) as symbols of grouping. The brackets contain their own sub-expressions (thus creating expressions within expressions). An example is:
3 (4 + 5) + 2.Here the sub-expression is 4 + 5. A more complicated example is:
10 (3 (4 + 5) + 2)It is the previous expression multiplied by 10. This expression contains a sub-expression which itself contains a sub-expression! The question then arises: in what order do we carry out these operations? The answer is given in this table:
Order of operations:
|
Thus the above examples would simplify like this:
Example: 4 + 5 · 2 3 → 4 + 5 · 8 → 4 + 40 → 44
Example: 3 (4 + 5) + 2 → 3 · 9 + 2 → 27 + 2 → 29
Example: 10 (3 (4 + 5) + 2) → 10 (3 · 9 + 2) → 10 (27 + 2) → 10 · 29 → 290
There are a couple of acronyms that people use to help them remember the order of operations table. One is BEDMAS, which stands for the order: Brackets, Exponentiation, Division and Multiplication, Addition and Subtraction.
Another one is PEMDAS, which stands for the order: Parentheses, Exponentiation, Multiplication and Division, Addition and Subtraction. Use whichever acronym you like better.
Invisible brackets
There are three locations where brackets are usually not shown but you have to imagine that they are there. One location is the exponent in an exponential. The other two are the numerator above a horizontal division line and the denominator below a horizontal division line. Here are two examples showing expressions, first with invisible brackets, and then with visible brackets (shown in red). We also show what the expressions evaluate to.Example 1:
In this exponential you know that the “+2” is in the exponent together with the “3” because it is written smaller and higher than the base and directly beside the “3”. This means that the exponent is meant to be “3+2” and must be kept together as if it had brackets around it.
Example 2:
In this fraction you know that the “+5” is in the numerator together with the “7” because it is written directly beside the “7” and the division line goes right across under both. The same goes for the “+4” in the denominator. This means that the numerator is “7+5” and the denominator is “2+4” and both must be kept together as if they had brackets around them.
Note:
- Compare the next two examples with the two examples above.
The only difference is that some of the numbers have been moved slightly or made bigger:
Conclusion: Neatness counts!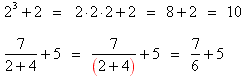
- In the above examples we could tell that a number was in the exponent or in the denominator by how big it was or where it was written. However, when typing one of these expressions into the Algebra Coach (or any other algebra program) you can't make the numbers smaller or higher. Everything must be typed in on a single line, so you must use brackets.