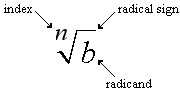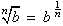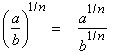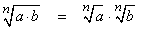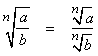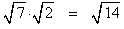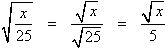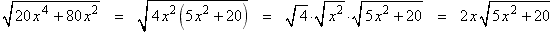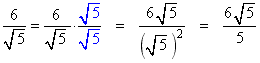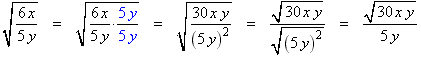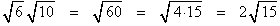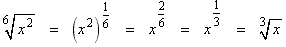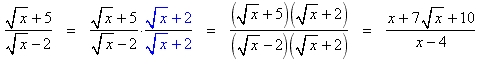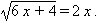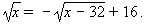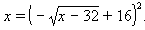Chapter 13 - Radicals and Radical Equations

This chapter discusses radicals. It contains the following sections:

section 13.1 - In this section we introduce radicals and talk about how to simplify them and do operations with them.
section 13.2 - In this section we explain how to solve radical equations.

13.1 - Simplifying Radicals

You may want to review the sections on integer exponents and exponents in general before you read this section.

Radical notation

Here is a picture of a radical defining its parts:

Note:

The index, n, must be a positive integer.
The above radical is spoken as “the n^th root of b”, for any index except n = 2 when we say “the square root of b” and n = 3 when we say “the cube root of b”.
An index of 2, for the square root, is usually not written.
The words “radical” and “root” will be used interchangably in this section.
The roots in this section have (almost) nothing to do with roots of an equation.

A radical is merely an alternative way to write an exponential whose exponent is a reciprocal . It is defined like this:

This means that for every property or rule that holds for an exponential there is a corresponding property or rule for a radical.

Root of a power and power of a root

A base raised to a fractional exponent m/n can be written in two ways in terms of radicals:

as the n^th root of the m^th power:
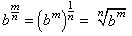
or as the m^th power of the n^th root:

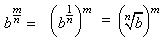
Note that the n^th power of the n^th root of any quantity and the n^th root of the n^th power of any quantity just equal that quantity:

and .

Thus the n^th power and the n^th root are inverse functions.

Root of a product or quotient

In section 3.3 we saw that a power of a product could be rewritten as a product of powers and a power of a quotient could be rewritten as a quotient of powers. For example:

and

This means that the root of a product can be rewritten as a product of roots:

and the root of a quotient can be rewritten as a quotient of roots:

Examples: The properties of radicals given above can be used to simplify the expressions on the left to give the expressions on the right.

Simplest form of a radical

A radical is said to be in simplest form (or standard form) when:

The radicand has been reduced as much as possible. (See the first example above.) This is done by removing factors from the radical.
There are no radicals in the denominator and no fractional radicands. This is done by rationalizing the denominator.
There are no products of radicals. (See the second example above.)
The index has been made as small as possible.

Removing factors from the radicand

Suppose that the index of the radical is n. Then factor the radicand so that one or more of the factors is a perfect n^th power. Then rewrite the root of the product as a product of roots and use the fact that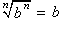

to simplify those factors. This process is called removing factors from the radicand.

Examples: All of the following are square roots. Therefore we look for perfect square factors in the radicand. In the first example the factor 25 is a perfect square. In the second example the factor x⁴ is a perfect square. In the third example we factor out 4 rather than 20 because 4 is a perfect square whereas 20 is not. In the last example the entire radicand is a perfect square.

Rationalizing the denominator

An expression is considered to be simpler when its denominator contains no radicals.

Suppose that the denominator of a fraction contains a square root. Then multiply both the numerator and denominator of the fraction by that square root and simplify. This may produce a radical in the numerator but it will eliminate the radical from the denominator. This process is called rationalizing the denominator.

Example: Simplify the expression

.

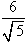Solution: Here are the steps:

Multiply the numerator and denominator by the square root of 5 (shown below in blue).
Multiply the fractions.
Use the fact that 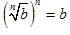. The result is a radical in the numerator but none in the denominator.

Suppose that a square root contains a fraction. Then multiply both the numerator and denominator of the fraction by the denominator of the fraction and simplify. This may produce a radical in the numerator but it will eliminate the radical from the denominator. This process is also called rationalizing the denominator.

Example: Simplify the expression

.

Solution: Here are the steps:

The square root contains a fraction and the denominator of the fraction is 5 y. Multiply the numerator and denominator of the fraction by 5 y (shown below in blue).
Multiply the fractions.
Convert the root of a quotient to a quotient of roots.
Use the fact that 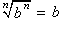. The result is a radical remaining in the numerator but none in the denominator.

Combining products of radicals

We saw above that the root of a product could be rewritten as a product of roots. Here we want to go the other way. It sometimes happens that converting a product of roots to the root of a product produces a perfect square factor and that factor can then be removed from the radicand.

Example: Simplify the expression

.

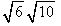Solution: Write this as the root of a product, namely of 60, and then notice that 60 has a perfect square factor of 4, which can then be removed from the radicand.

Reducing the index

It is sometimes possible to reduce the index by writing the radical in exponential form and then reducing the fractional exponent to lowest terms.

Example: Simplify the expression

.

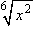Solution: Write this in exponential notation and use the exponentiation property of exponents to give the single exponent 2/6 and then reduce the fraction 2/6 to 1/3.

Binomial denominators containing radicals

Suppose that the denominator of a fraction is a binomial (i.e. it contains two terms) and that one or both of those terms is a radical. Then multiplying the numerator and denominator of the fraction by the binomial conjugate of the denominator and distributing will eliminate all radicals from the denominator. (Note that the binomial conjugate of the binomial a + b is the binomial a − b and vice versa.

Example: Eliminate the radical from the denominator of the expression

.

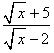Solution: Follow these steps:

Multiply the numerator and denominator by the binomial conjugate of the denominator (shown below in blue).
Multiply the fractions.
Distribute in the numerator. In general the radicals survive. Distribute in the denominator. The cross-terms cancel so that the radicals disappear, which is the whole point of using the binomial conjugate.

13.2 - Radical Equations

Before reading this section you may want to review the following topics:

A radical equation is one in which the unknown, call it x, is inside a radical. To solve a radical equation follow these steps:

Isolate the term containing the radical on one side of the equation, say on the left-hand-side. (By isolate we mean get it by itself.)
If the radical is a square root then square both sides of the equation. (In general, if the radical is an n^th root then take the n^th power of both sides.) On the left-hand-side use the fact that 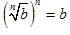to get rid of the radical. On the right-hand-side distribute.
The unknown x is no longer inside a radical. Now you can finish solving for x by using the basic procedures for solving equations.

Note:

If the equation contains more than one radical term, you will have to perform the above procedure several times.
One of the steps, squaring both sides of the equation, increases the degree of the unknown, and this often leads to extraneous solutions. Therefore it is very important to check your solutions.

Example: Solve the radical equation

.

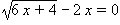Solution: The first step is to isolate the radical term:

Then square both sides:

6 x + 4 = 4 x².

The result is that this is no longer a radical equation; it is a quadratic equation. Divide both sides by 2 to simplify it and then collect all terms on one side of the equation to put it into standard form:

2 x² − 3 x − 2 = 0.

Click here to see how the left-hand-side of this quadratic equation can be factored. The result is this:

(x − 2) (2 x + 1) = 0.

The purpose of factoring is to put the equation into the form a · b = 0. We can now replace it with two new equations. Each new equation comes from setting one of the factors to zero:

x − 2 = 0
2 x + 1 = 0

Their solutions are x = 2 and x = −½. We must check these solutions. Substituting x = 2 into the original equation and simplifying causes the equation to read 0 = 0, so this solution checks out. But substituting x = −½ back into the original equation causes it to read 2 = 0, so this solution doesn’t check out and must be rejected. Thus this radical equation has the single solution x = 2.

Example: Solve the radical equation

.

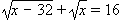Solution: The first step is to isolate one of the radical terms (it doesn’t matter which one):

Then square both sides:

On the left-hand-side squaring got rid of the radical. On the right-hand-side we will have to distribute. After distributing and collecting like terms we get this equation:

This is still a radical equation because although one radical is gone, the other one still remains. So we repeat the entire process. Isolate the remaining radical term (by canceling x terms and dividing by 32):

Then square both sides:

x − 32 = 49

Note that this is no longer a radical equation; both radicals are now gone. Solving this equation yields the solution x = 81. We must now check the solution. Substituting x = 81 back into the original equation and simplifying gives the equation 16 = 16, so this solution checks out.