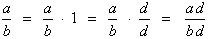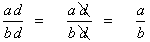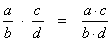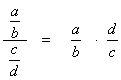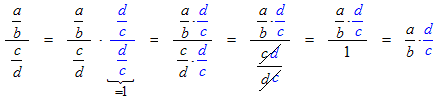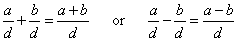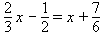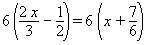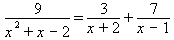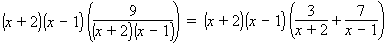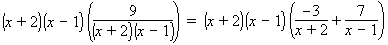Chapter 11 - Fractions and Fractional Equations

In this chapter we look at fractions for the fourth and last time. Let’s review our previous three encounters:

Common fractions. In section 1.2 we introduced the fraction notation, a/b, where a and b were both integers to describe a fraction or part of a whole object. For example ¾ meant that we had broken an object into 4 equal parts and we had 3 of those parts. Note that a/b was a number; the notation a/b had nothing to do with division. In section 1.2 we also learned how to reduce a fraction to lowest terms, how to add and subtract fractions, multiply fractions, divide fractions, and how to convert an improper fraction to a mixed fraction using long division.
Division of numbers. In section 2.4 we defined the division of two numbers in terms of multiplication. We said that dividing a by b produced a number c such that c multiplied by b gave back a. We used the same fraction notation, a/b, to denote the division of a by b because when a and b were both integers, then the division a/b resulted in the common fraction a/b. In any other case, though, the division resulted in a real number. In section 2.4 we also learned that the division of a by b could be replaced by the multiplication of a by the reciprocal of b. Finally, we learned the rules for division involving minus signs.
Division of expressions. In section 3.5 we saw that there were three different ways to divide expressions, depending on whether the numerator, a, and denominator, b, were monomials, multinomials or polynomials.
- If they were monomials, then dividing a by b simply amounted to writing down the algebraic fraction, a/b, and reducing it to lowest terms, just like a common fraction.
- If they were polynomials, then a could be divided by b using long division, just like an improper common fraction could be converted to a mixed fraction using long division.
- If a was a multinomial and b was a monomial then we placed each term of a over b so that the result of the division was a sum of algebraic fractions.

What remains to be discussed are algebraic fractions, which are fractions whose numerator and denominator are algebraic expressions. This chapter discusses algebraic fractions and fractional equations. It contains the following sections:

section 11.1 - In this section we talk about the simplification of algebraic fractions. The main new result is that since we now know how to factor an expression, we can factor a numerator or denominator, and this opens up a new way to reduce an algebraic fraction to lowest terms.
section 11.2 - In this section we talk about the multiplication and division of algebraic fractions.
section 11.3 - In this section we talk about the addition and subtraction of algebraic fractions.
section 11.4 - In this section we show how to solve equations containing algebraic fractions.

11.1 - Simplification of algebraic fractions

Some definitions

A common fraction is a number that is written in the form 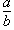or a/b, where a, the numerator, and b, the denominator, are both integers. A common fraction is used to describe a part or fraction of a whole object. The notation means that we break an object into b equal parts and we have a of those parts. The portion or fraction of the object that we have is a/b.
Division is defined in terms of multiplication. Dividing a number a by a number b produces a number c such that c multiplied by b gives back a. We use the same fraction notation, a/b, to denote the division of a by b because when a and b were both integers, then the division a/b results in the common fraction a/b.
An algebraic fraction is one whose numerator or denominator are algebraic expressions. Two examples of algebraic fractions are
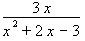and .
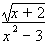A rational algebraic fraction is an algebraic fraction whose numerator and denominator are both polynomials. The first example above is a rational algebraic fraction; the second one is not.
A proper common fraction is a common fraction whose numerator is smaller than its denominator, and an improper common fraction is one whose numerator is greater than or equal to its denominator. A mixed fraction is the sum of an integer and a proper fraction. Long division can be used to convert an improper fraction to a mixed fraction.
A proper algebraic fraction is a rational algebraic fraction whose numerator is of lower degree than its denominator, and an improper algebraic fraction is one whose numerator is of greater or equal degree than its denominator. A mixed expression is the sum of a polynomial and a proper algebraic fraction. Long division can be used to convert an improper algebraic fraction to a mixed expression.

Division by zero

This operation is not allowed in mathematics. Click here to see why. This means that in the algebraic fraction

,

x cannot equal 1 or −3 because those values of x would cause the fraction to have a denominator of zero.

Reducing an algebraic fraction to lowest terms

Look at the algebra that we do here:

We start with the fraction a/b.
We multiply it by 1. This will not change its value.
We write the ‘1’ as the fraction d/d.
We multiply the two fractions. The numerator of the new fraction is ad and the denominator is bd.
The final fraction is equivalent to the first fraction.

If we go in the reverse direction then we say that we are reducing a fraction to its simplest equivalent fraction or to lowest terms. To accomplish this we find any factor that is contained in both the numerator and denominator and cancel it out or strike it out, like this:

Example: Reduce the common fractions 10/6 and 10/5 to lowest terms.

	Factor the numerator and denominator. Cancel the common factor of 2.
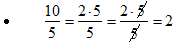	Factor the numerator and denominator. Cancel the common factor of 5. The result of the division is an integer. We say that the denominator divides evenly into the numerator.

If the numerator and denominator of an algebraic fraction are both monomials, then take all of the following steps to reduce the fraction to lowest terms:

Obtain the sign by using the rules for signs.
Reduce the coefficient to lowest terms.
Cancel identical factors that appear in both the numerator and denominator.
Combine exponentials having the same base by using the division property of exponentials.

Example: Reduce the algebraic fraction

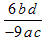to lowest terms.
Solution:

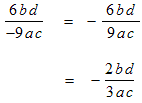The − sign is put either in front of the result or in front of the numerator; never in front of the denominator.

Reduce the coefficient 6/9 to lowest terms.

Example: Reduce the algebraic fraction

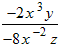to lowest terms.
Solution:

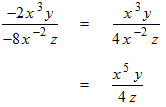The two − signs are replaced by a + sign which we don’t have to display. The coefficient reduces to ¼. The numerator contains other factors so the 1 in the numerator can be omitted.

Combine the exponentials with base x using the properties of exponents.

Example: Reduce the algebraic fraction

to lowest terms.
Solution:

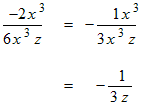The − sign is put in front. The coefficient reduces to 1/3. The identical factors of x³ in the numerator and denominator cancel. The numerator contains no other factors so this time the 1 must be displayed.

Example: Reduce the algebraic fraction

to lowest terms.
Solution:

After carrying out all the simplifications, the denominator equals 1, so we don’t have to display it. Thus the result is an ordinary expression, not an algebraic fraction.

If the numerator and denominator of an algebraic fraction are both multinomials, then in addition to the steps listed above, try the following steps to reduce the fraction to lowest terms:

Factor the numerator or denominator or both. Sometimes this will cause new canceling factors to appear.
Factor a − sign out of the numerator or denominator. Sometimes this will cause a new canceling factor to appear.

In the following examples we will assume that you already know how to do the factoring so we will just show how to use the factors to reduce the algebraic fractions to lowest terms.

Example: Reduce the algebraic fraction

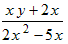to lowest terms.
Solution:

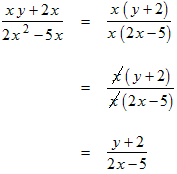Factor the numerator and denominator.

Cancel the common factor of x.

Example: Reduce the algebraic fraction

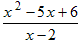to lowest terms.
Solution:

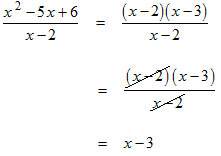
Factor the numerator.

Cancel the common factor of x − 2.

Example: Reduce the algebraic fraction

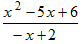to lowest terms.

Solution: This is the same algebraic fraction as in the previous example except that the denominator differs by a − sign.

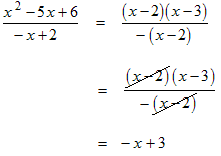Factor the numerator and factor a − sign out of the denominator.

Cancel the common factor of x − 2.

Bring the − sign to the numerator and distribute it.

11.2 - Multiplication and division of algebraic fractions

Multiplication of algebraic fractions

The procedure for multiplying algebraic fractions is the same as the procedure for multiplying common fractions.

Multiplying two algebraic fractions produces a new algebraic fraction. Multiply the two numerators to get the new numerator and multiply the two denominators to get the new denominator:

Then simplify by reducing the new fraction to lowest terms.

Examples:

Division of algebraic fractions

The procedure for dividing algebraic fractions is the same as the procedure for dividing common fractions.

Replace the division by a fraction by the multiplication by the reciprocal of that fraction, like this:

Then carry out the multiplication of the two fractions as described above.

Notice that you take the reciprocal of the fraction on the bottom!

Here is why this procedure works:

The key is that instead of seeing a fraction divided by a fraction, look for a single fraction whose numerator and denominator just happen to be fractions. In the first step we multiplied this fraction by a UFOO whose numerator and denominator just happen to be fractions. The UFOO was chosen so the fractions in the denominator would cancel and give 1. After another simplification that left only the final multiplication of fractions.

Examples: Look for these three steps: (1) invert the bottom fraction, (2) multiply the fractions, (3) simplify.

11.3 - Addition and subtraction of algebraic fractions

The procedure for adding or subtracting algebraic fractions is the same as the procedure for adding or subtracting common fractions.

Adding fractions with equal denominators

Factions that have equal denominators are also called like fractions.

To add or subtract two like fractions, simply add or subtract the numerators and put the result over the common denominator, like this:

Example:

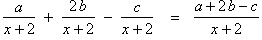
Adding fractions with unequal denominators

To add or subtract fractions don’t have equal denominators, they must first be converted to equivalent fractions that do have a common denominator. Here are the steps:

Find the lowest common multiple of the denominators. When applied to fractions this number is called the lowest common denominator (LCD) of the fractions.
Convert each fraction to an equivalent fraction that has the LCD as its denominator. To do this, multiply the numerator and denominator of each fraction by the appropriate factor that makes this happen.
Add the numerators and place over the common denominator.
Simplify the result by reducing it to lowest terms.

Example:

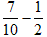. To subtract these fractions, the steps are:

Find the LCD, which is 10.
Since the first fraction already has the LCD as its denominator, we need only multiply the second fraction by 5/5 to convert it to an equivalent fraction with a denominator of 10.
Subtract the numerators and place the result over the LCD.
Simplify by reducing the fraction to lowest terms.

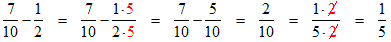
Example:

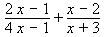. To add these fractions, the steps are:

Find the LCD, which is (4 x − 1)(x + 3).
Multiply the numerator and denominator of the first fraction by (x + 3) and the numerator and denominator of the second fraction by (4 x − 1):
The two fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.
Simplify by distributing the numerator.

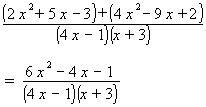
Adding fractions with factorable denominators

You must always factor the denominators. This is the only way to tell if a factor appears in more than one denominator.

Example:

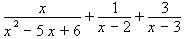. To add these fractions, the steps are:

Factor the denominator of the first fraction. Then we can see that the factors x − 2 and x − 3 appear in more than one denominator:
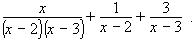
Find the LCD, which is (x − 2)(x − 3).
Multiply the numerator and denominator of the second fraction by (x − 3) and the numerator and denominator of the third fraction by (x − 2):
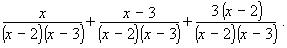
The three fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.
Simplify by distributing and adding like terms in the numerator.

Adding fractions and non-fractions (mixed expressions)

To add or subtract fractions and non-fractions, convert the non-fractions into fractions with denominators of 1.

Example:

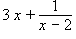. To add this fraction and non-fraction, the steps are:

Write the non-fraction as a fraction with a denominator of 1:
Find the LCD, which of course, is (x − 2).
Multiply the numerator and denominator of the first fraction by (x − 2):
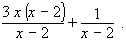
The two fractions now both have the LCD as their denominator. Add the numerators and place the result over the LCD.
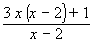
Simplify by distributing and adding like terms in the numerator.

11.4 - Fractional equations

Before reading this section you may want to review the following topics:

The basics of solving equations.
The technique of clearing fractions for solving linear equations.
How to find the lowest common denominator (LCD) of algebraic fractions.

A fractional equation is one that contains fraction terms. In section 4.2 we saw how to solve a linear equation that contains fractions. The steps for solving any fractional equation are exactly the same:

Look at the denominators of all the fraction terms and find their lowest common multiple (LCM) (this is also called the lowest common denominator (LCD) of the fractions).
Multiply both sides of the equation by the LCM.
Distribute the LCM over both sides of the equation.
The equation no longer contains fraction terms and you can continue solving it by using the basic procedures for solving equations.
Check the solution. This is especially important with fractional equations. There are two possible problems:
- If the denominator of any fraction term contains x, then the LCM will also contain x, and multiplying both sides of the equation by the LCM will increase the degree of x in the equation. This often leads to extraneous solutions.
- When substituting the solutions back into the original equation to check them, any solution that causes any fraction term to have a denominator of zero must be dropped because division by zero is forbidden in mathematics.

Example 1: Solve this fractional equation for x:

Solution: The fraction terms have denominators of 3, 2 and 6. The LCM of these numbers is 6. Multiply both sides of the equation by 6. (Don’t forget to put brackets around both sides of the equation.)

Distribute on both sides of the equation:

4 x − 3 = 6 x + 7.

The fractions are now cleared so this is no longer a fractional equation. Finish solving the equation by collecting linear terms on the left-hand-side and constant terms on the right-hand-side. This gives:

−2 x = 10.

Divide both sides by −2. This gives the solution:

x = −5.

Check it by substituting it back into the original equation. This gives −23 / 6 = −23 / 6, so the solution checks out.

Example 2: Solve this fractional equation for x:

Solution: The fraction terms have denominators of x² + x − 2, x + 2, and x − 1. It might appear that the LCM is just the product of all three, but because x² + x − 2 can be factored as (x + 2)(x − 1), the LCM is actually just (x + 2)(x − 1). Multiply both sides of the equation by it. (Don’t forget to put brackets around both sides of the equation.)

Distribute on both sides of the equation:

9 = 3 (x − 1) + 7 (x + 2).

The fractions are now cleared so this is no longer a fractional equation; it is a linear equation. Solve it using the usual techniques. Distribute once more on the right-hand-side:

9 = 10 x + 11.

Collect constant terms on the left-hand-side:

−2 = 10 x.

Divide both sides by 10. This gives the solution:

x = −1/5.

Check it by substituting it back into the original equation. This gives −25 / 6 = −25 / 6, so the solution checks out.

Example 3: The purpose of this example is to illustrate a solution that must be rejected because it causes a division by zero. The equation is identical to the one in the previous example except that it differs in the sign of one term. Solve this fractional equation for x:

Solution: Compare each step here with the corresponding step in the example above. Multiply both sides of the equation by the LCM, which again is (x + 2)(x − 1):

Distribute on both sides of the equation:

9 = −3 (x − 1) + 7 (x + 2).

Distribute once more on the right-hand-side:

9 = 4 x + 17.

This time the solution is x = −2. If we try to substitute it back into the original equation we get divisions by zero in two of the fractions. Therefore we must reject this solution and state that the equation has no solution.