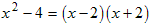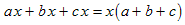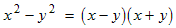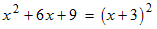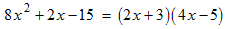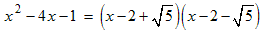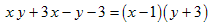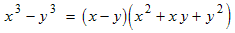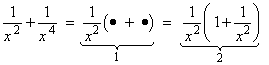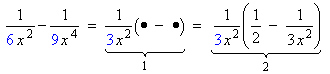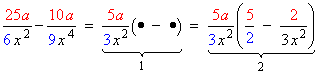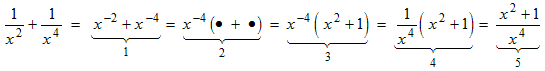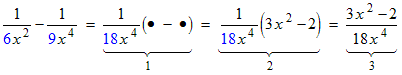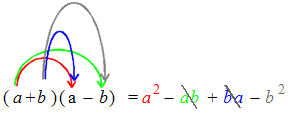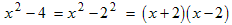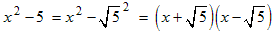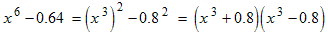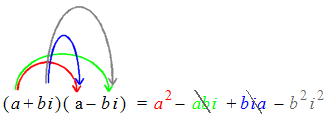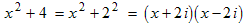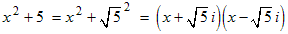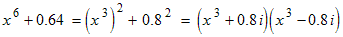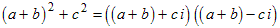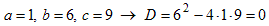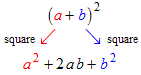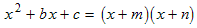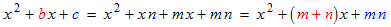Chapter 8 - Factoring
Before you begin to learn about factoring expressions you may want to review factoring numbers, because factoring expressions is based on it. Also you previously learned how to multiply expressions. Factoring is the reverse process, in that you find those quantities that would be multiplied to give some expression. So you may want to review that topic as well.Before learning about factoring you might want to know what it's good for. Factoring is required for:
- Simplifying expressions; for example combining like terms.
- Solving equations; for example quadratic equations.
- Simplifying fractions and simplifying algebraic fractions.
- Adding common fractions and adding algebraic fractions.
- Completing the square.
Some definitions:
|
Example: The prime factors of the monomial 5 a x 2 are obviously 5, a, x and x. Factoring monomials is so simple we discuss them no further. From now on we will assume that we want to factor multinomials.
Example: The factors of the expression a x + b x are x and a + b, because the expression can be written as the product of the factors, like this:
a x + b x = x (a + b)You can verify that this is correct by multiplying out the factored expression on the right side and obtaining the original expression on the left side.
Example: The factors of x 2 − 4 are x − 2 and x + 2, because:
Again, you can verify that this is correct by multiplying out the factored expression on the right side and obtaining the original expression on the left side.
Example: The expressions x − 2 and x + 2 are prime, but as the previous example shows, the expression x 2 − 4 is factorable.
Factoring an expression is done by recognizing the form of the expression and then applying the rules for factoring that form. The following table gives the names of the factorable forms and an example of each. The left side of the example shows the expression before factoring and the right side shows the expression after factoring. The forms are ordered more or less from the simplest to the hardest to factor. This is the order in which the Algebra Coach tests an expression for factorability. Click on any form to see how it is factored.
Factorable form or method used Example Common factor Difference of squares Quadratic trinomial, perfect square Quadratic trinomial, a = 1 Quadratic trinomial, a ≠ 1 Completing the square Grouping Sum or difference of cubes Polynomial
8.1 - Factoring expressions with common factors
This is the easiest form to factor. An expression is of this form if each term of the expression contains the same quantity, called the common factor. This quantity is factored out using the distributive law. Here are some examples:Example 1: Factor a x − b x
Each term of this expression contains a factor of x, so this is a common factor. The distributive law allows us to write this in the factored form:
a x − b x = x (a − b)
Example 2: Factor x 3 + 3 x
Again each term contains the common factor of x. The distributive law allows us to write this as:
x 3 + 3 x = x (x 2 + 3)In this example we also had to make use of the multiplication property of exponents to write x 3 = x · x 2. In general, if various terms have various powers of x then the lowest power of x is the common factor.
Example 3: Factor
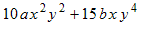
This expression is more complicated so we will factor it in two steps.
- The first step is to find the common factor.
The two terms contain the numbers 10 and 15, whose
greatest common factor is 5,
so the common factor must contain 5.
Both terms contain x so the common factor must contain x.
Both terms contain y so the common factor must contain
the lowest power of y, namely y 2.
Thus we can write the factored form of the expression like this:
where the two • quantities that remain inside the brackets are yet to be determined.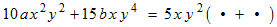
- The second step is to determine the • quantities. As in
Example 2 this is done using the
multiplication property of exponents
for both x and y. The result is that we can write the expression
in factored form like this:
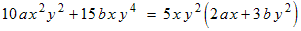
Common factors in the denominator
If an expression is made up of fractions and if every fraction’s denominator contains the same quantity, then that quantity can also be factored out with the distributive law.Example 4: Factor
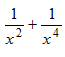
Here are the steps:
- One denominator is x2 and the other denominator is x4 and their common factor is x2. We put this in the factor’s denominator. The • quantities are yet to be determined.
- Use the properties of exponents to determine the • quantities.
Example 5: Factor

Here are the steps:
- Find the common factor in the denominators. It is 3x 2 and we put this in the factor’s denominator. The • quantities are yet to be determined.
- Use the distributive law to determine the • quantities.
Example 6: Factor
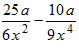
This example adds another complication to the previous two examples (namely the quantities shown below in red) so study those examples first. Here are the steps:
- Find the common factor. As in the previous example it contains 3x 2 in the denominator but what is new is the quantity 5a shown in red. The • quantities are yet to be determined.
- Determine the • quantities inside the brackets. The red and blue quantities match with the red and blue quantities in the original expression.
‘Uncommon’ Common Factors
Sometimes it is desirable to factor out some quantity from an expression even if not every term contains that quantity. The usual reason is to achieve some desired form. Here are some examples:Example 7: Suppose that we want to apply the completing-the-square process (this is covered in the next chapter ) to the quadratic 2 x 2 + 9 x − 20. The problem is that this process requires that we start with a quadratic of the form x 2 + b x + c. (That is, the coefficient of the x 2 term must be 1.) To achieve this we factor out 2. Then we can complete the square on the quadratic that remains inside the brackets. Here are the steps:
- We want the factor to be 2. The • quantities are yet to be determined.
- We use the distributive law to determine the • quantities inside the brackets.
- Now we are ready to complete the square on the quadratic inside the brackets.
Example 8: Express
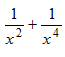 using exponential notation and factor out the lowest power of x.
using exponential notation and factor out the lowest power of x.
Here are the steps:
- Rewrite the denominators using negative exponents. Notice that the lowest power of x is −4.
- Factor out x to the lowest power. The • quantities are yet to be determined.
- Use the properties of exponents to determine the • quantities.
- Optional. Use the negative exponent property to rewrite the common factor as a fraction.
- Optional. Simplify by moving the bracketted quantity into the numerator. Now we see that the result is exactly the same as adding fractions by finding a common denominator!
Example 9: In Example 5 we used the GCF (greatest common factor) of the denominators of
 as the denominator of the common factor. In this example we will instead use the
LCM
(lowest common multiple). Here are the steps:
as the denominator of the common factor. In this example we will instead use the
LCM
(lowest common multiple). Here are the steps:
- The LCM of 6 x 2 and 9 x 4 is 18 x 4 and we put this in the factor’s denominator. The • quantities are yet to be determined.
- Determine the • quantities inside the brackets.
- Optional. Move the bracketted quantity into the numerator. Again we see that the result is exactly the same as adding fractions by finding the LCD.
8.2 - Factoring a difference of squares
Just as the name suggests, a difference of squares is an expression of the form: a 2 − b 2.A difference of squares can be factored like this: a 2 − b 2 = (a + b) (a − b). |
You can easily verify this by multiplying out the right hand side and noticing that the cross terms cancel:
Here are some examples showing the range of expressions that qualify as a difference of squares.
Example: Factor x 2 − 4.
The second term can be thought of as the square of the number 2:
Example: Factor x 2 − 5.
The second term can be thought of as the square of the square root of 5:
Example: Factor x 6 − 0.64.
The first term can be thought of as the square of x 3:
Example: Factor (a + b) 2 − c 2.
In this case the first term is the multinomial (a + b):
You should now simplify by dropping the unnecessary brackets and get
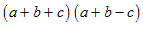 .
.Factoring a sum of squares over the complex numbers
Similar to a difference of squares, a sum of squares is an expression of the form: a 2 + b 2.A sum of squares cannot be factored over the real numbers but over the complex numbers it can be factored like this: a 2 + b 2 = (a + b i ) (a − b i ),where 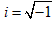 . .
|
You can easily verify this by multiplying out the right hand side and then canceling the cross terms:
and then simplifying the last term to +b 2 because i 2 = −1.
Here are some examples showing the range of expressions that qualify as a sum of squares.
Example: Factor x 2 + 4.
The second term can be thought of as the square of the number 2:
Example: Factor x 2 + 5.
The second term can be thought of as the square of the square root of 5:
Example: Factor x 6 + 0.64.
The first term can be thought of as the square of x 3.
Each factor can actually be factored further than is shown here. Click here to see how.
Example: Factor (a + b) 2 + c 2.
In this case the first term is the multinomial (a + b):
You should now simplify by dropping the unnecessary brackets and get
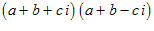 .
.8.3 - Factoring quadratic trinomials
Definitions: A quadratic trinomial is an expression of the form: a x 2 + b x + c,where x is a variable and a, b and c are non-zero constants. The constant a is called the leading coefficient, b is called the linear coefficient, and c is called the additive constant. The discriminant, D, of a quadratic trinomial is defined as the quantity: D = b 2 − 4 a c.The discriminant is used to classify or discriminate among various cases of quadratic trinomials. A perfect square number is a number that is the square of some integer. We will be interested in knowing whether or not the discriminant is a perfect square. |
Example: The expression:
x 2 + 7 x + 6.is a quadratic trinomial with coefficients a = 1, b = 7, and c = 6. The discriminant is D = 7 2 − 4 · 1 · 6 or D = 25. D is a perfect square because it is the square of 5.
Example: The expression:
2 x 2 + 3 x − 4.is a quadratic trinomial with coefficients a = 2, b = 3, and c = −4. The discriminant is D = 3 2 − 4 · 2 · (−4) or D = 41. Notice that D is not a perfect square.
Note: If b or c is zero then the quadratic is said to be an incomplete quadratic and if a is zero then the expression isn’t even quadratic; it is linear. If any of the coefficients a, b or c is zero then the expression is no longer a trinomial and should be factored (assuming that it is factorable) by one of the simpler methods that we have studied previously:
- If c = 0, then a x 2 + b x has a common factor, namely x.
- If b = 0, then, depending on whether c is positive or negative, a x 2 + c is either a sum or difference of squares.
- If a = 0, then b x + c is linear, not quadratic, and can only have a number as a common factor.
Assumptions for this section: We will assume that the coefficients a, b and c are all non-zero integers and that the discriminant, D, is a perfect square. If these conditions don't hold then the quadratic trinomial cannot be factored by the methods of this section but may still be factorable using the more complicated method of completing the square. |
If these conditions do hold then there are three possible cases for the quadratic trinomial, each of which is factored by a different method:
- discriminant D = 0 (trinomial is a perfect square)
- discriminant D ≠ 0 and leading coefficient a = 1
- discriminant D ≠ 0 and leading coefficient a ≠ 1 (use the grouping method)
Factoring perfect square quadratic trinomials
In this section we learn how to factor perfect square quadratic trinomials. These are quadratic trinomials that can be written as the square of some expression. Here are some examples of perfect square trinomials in unfactored and factored form:Note that the second example can be considered to be a quadratic trinomial because we can let x play the role of the variable and let y be a constant. The discriminant, D, is always zero for perfect square trinomials. If you calculate the discriminant for the first example you find that:
and for the second example:
It is convenient to write a perfect square quadratic trinomial in the form: a 2 + 2 a b + b 2Then it can be factored like this: a 2 + 2 a b + b 2 = (a + b) 2 |
You can verify this by distributing the right hand side of the above equation and obtaining the left hand side:
Notice that the first and last terms of the trinomial are obtained by squaring the first and last terms of the factored form:
and that the middle term of the trinomial is obtained by taking twice the product of the first and last terms of the factored form:
This leads to the following procedure for factoring a perfect square trinomial:
|
Example: Factor
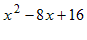
- Verify that this is a perfect square trinomial by checking that D = 0:
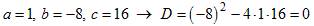
- Tentatively factor the trinomial like this (? means either + or −):
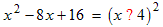
- The middle term has the opposite sign of the first and last terms so
the result is:
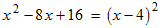
Example: Factor
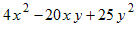
- Verify that this is a perfect square trinomial by checking that D = 0:
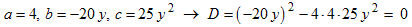
- Tentatively factor the trinomial like this
(? means either + or −):

- The middle term has the opposite sign of the first and last terms so
the result is:
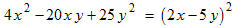
Factoring quadratic trinomials when a = 1
In this section we learn how to factor a quadratic trinomial whose leading coefficient is a = 1:x 2 + b x + c.(We also assume that b and c are integers and that the discriminant is a perfect square.) First notice that the factors must be binomials, both of whose x terms must have coefficients of 1:
(x + •) (x + •)Now we need to determine the two • quantities. Let's call them m and n and set the unfactored form equal to the factored form:
If we distribute the right side and then combine like terms we get:
The only way that the left side can be identical to the right side is if:
b = m + n, and c = m n.(In words, the sum of m and n must equal b and the product of m and n must equal c.) It is easy to show that only one combination of m and n will satisfy both conditions. Also, we will see in the section on completing the square that m and n are guaranteed to be integers if the discriminant D is a perfect square.
This leads to the following procedure for factoring a quadratic trinomial a x 2 + b x + c when a = 1:
|
Example: Factor x 2 + 8 x + 12
- For this trinomial a = 1, b = 8 and c = 12,
and the discriminant is
D = b 2 − 4 a c =
8 2 − 4 · 1 · 12 =
16, which is a perfect square, namely 4 2.
- Tentatively write the trinomial in the factored form:
x 2 + 8 x + 12 = (x + m) (x + n)
- Now find m and n. They are integers that satisfy the conditions:
m n = 12, and m + n = 8.
Here is a list of all the pairs of integers whose product is 12. Pick the pair whose sum is 8.
Thus m = 6 and n = 2 and the expression factors as:m n 12 1 6 2 ← this pair has a sum of 8 4 3 3 4 ← already checked 2 6 ← already checked 1 12 ← already checked x 2 + 8 x + 12 = (x + 6) (x + 2)
Example: Factor x 2 + x − 12
- For this trinomial a = 1, b = 1 and c = −12,
and the discriminant is
D = b 2 − 4 a c =
1 2 − 4 · 1 · (−12) =
49, which is a perfect square, namely 7 2.
- Tentatively write the trinomial in the factored form:
x 2 + x − 12 = (x + m) (x + n)
- Now find m and n. They are integers that satisfy the conditions:
m n = −12, and m + n = 1.
Here is a list of some of the pairs of integers whose product is −12. Pick the pair whose sum is 1.
Thus m = 4 and n = −3 and the expression factors as:m n 12 −1 6 −2 4 −3 ← this pair has a sum of 1 … … ← need check no further x 2 + x − 12 = (x + 4) (x − 3)
Factoring quadratic trinomials when a ≠ 1 using the grouping method
In this section we learn how to factor a quadratic trinomial whose coefficients a, b and c can be any integers:a x 2 + b x + c.(Thus a no longer has to be equal to 1 as in the previous section but we still assume that the discriminant is a perfect square.) The method that we develop is a variation of the grouping method. Start by assuming that the quadratic trinomial can be factored like this:
a x 2 + b x + c = (p x + q) (r x + s).We now set out to find p, q, r and s. Distribute on the right hand side:
a x 2 + b x + c = p r x 2 + p s x + q r x + q s.Look at the blue and red numbers on the right hand side. Think of p r as a single number (that has factors p and r), think of p s as another number that can be factored, and so on. Then, just as in the previous case, one condition for the left side to be equal to the right side is that:
b = p s + q r.In words, the sum of the number p s and the number q r must equal b. Unlike the previous case, the second condition is on the product a c. It is that:
a c = p r · q s = (p s) (q r).In words, the product of the number p s and the number q r must equal the product of a and c. These two conditions together give us enough information to find the two numbers p s and q r. We will see in the section on completing the square that these two numbers are guaranteed to be integers if the discriminant D is a perfect square. Also it can be shown that they are unique.
Now use the two numbers p s and q r as a guide to split up the x term of the trinomial into two terms, like this:
a x 2 + b x + c = a x 2 + p s x + q r x + c,or, showing the factors of a and c, like this:
a x 2 + b x + c = p r x 2 + p s x + q r x + q s.Now make two groups on the right hand side (hence the name grouping method). The first group consists of the first two terms (shown in red) and the second group consists of the last two terms (shown in blue):
a x 2 + b x + c = p r x 2 + p s x + q r x + q s.Factor one common factor out of the first group and a different common factor out of the last group like this:
a x 2 + b x + c = p x(r x + s) + q(r x + s).This causes a new common factor of r x + s to appear, which we can also factor out, and we are done:
a x 2 + b x + c = (p x + q) (r x + s).
This leads to the following procedure for factoring a quadratic trinomial a x 2 + b x + c when a ≠ 1:
|
Example: Factor 6 x 2 + 7 x − 5
- For this trinomial a = 6, b = 7 and c = −5,
and the discriminant is
D = b 2 − 4 a c =
7 2 − 4 · 6 · (−5) =
169, which is a perfect square, namely 13 2, so the conditions are met
for the grouping method to work.
- Find integers m and n that satisfy the conditions:
m n = a c = −30, and m + n = b = 7.
Here is a list of all the pairs of integers whose product is −30. Pick the pair whose sum is 7.m n 30 −1 15 −2 10 −3 ← this pair has a sum of 7 6 −5 … … ← need check no further; rest of list duplicates previous rows - Use the two numbers m = 10 and n = −3 as a guide to split up
the x term of the trinomial into two terms:
6 x 2 + 7 x − 5 = 6 x 2 + 10 x − 3 x − 5.
- Think of this as two groups, each consisting of two terms:
6 x 2 + 7 x − 5 = 6 x 2 + 10 x − 3 x − 5.
Factor the common factor 2 x out of the first group and a − sign out of the last group:6 x 2 + 7 x − 5 = 2 x(3 x + 5) − (3 x + 5).
- Now factor out the new common factor 3 x + 5, and we are done:
6 x 2 + 7 x − 5 = (2 x − 1) (3 x + 5).
Example: Factor 8 x 2 + 2 x − 15
- For this trinomial a = 8, b = 2 and c = −15,
and the discriminant is
D = b 2 − 4 a c =
2 2 − 4 · 8 · (−15) =
484, which is a perfect square, namely 22 2, so the conditions are met
for the grouping method to work.
- Find integers m and n that satisfy the conditions:
m n = a c = −120, and m + n = b = 2.
Here is a list of all the pairs of integers whose product is −120. Pick the pair whose sum is 2.m n 120 −1 60 −2 40 −3 30 −4 24 −5 20 −6 15 −8 12 −10 ← this pair has a sum of 2 … … ← need check no further; rest of list duplicates previous rows - Use the two numbers m = 12 and n = −10 as a guide to split up
the x term of the trinomial into two terms:
8 x 2 + 2 x − 15 = 8 x 2 + 12 x − 10 x − 15.
- Think of this as two groups, each consisting of two terms:
8 x 2 + 2 x − 15 = 8 x 2 + 12 x − 10 x − 15.
Factor the common factor 4 x out of the first group and −5 out of the last group:8 x 2 + 2 x − 15 = 4 x(2 x + 3) − 5(2 x + 3).
- Now factor out the new common factor 2 x + 3, and we are done:
8 x 2 + 2 x − 15 = (2 x + 3) (4 x − 5).
8.4 - Factoring by grouping
This is probably the hardest factorable form to identify. It is largely a matter of trial and error and about the only thing that can be said for sure is that the expression to be factored has to have at least four terms. The idea is that it may be possible to arrange the terms into groups, each of which can be factored separately. This may cause the groups to have a new common factor which can be factored out. (This is a lot of maybe’s!) Here are some examples:Example: Factor x y + 3 x + 2 y + 6
The first two terms form a group and the last two terms form another group. Factor x out of the first two terms and 2 out of the last two terms:
x(y + 3) + 2(y + 3).Now the two groups have a common factor of y + 3. Factor out that common factor. This gives:
(x + 2) (y + 3).
Example: Factor a 2 c + a 2 d − c − d
The first two terms form a group and the last two terms form another group. Factor a 2 out of the first two terms and a − sign out of the last two terms:
a 2(c + d) − (c + d).Now the two groups have a common factor of c + d. Factor out that common factor. This gives:
(a 2 − 1)(c + d).
8.5 - Factoring a sum or difference of cubes
Just as the names suggest, a sum of cubes is an expression of the form: a 3 + b 3,and a difference of cubes is an expression of the form: a 3 − b 3.A sum of cubes can be factored like this: a 3 + b 3 = (a + b) (a 2 − a b + b 2 ),and a difference of cubes can be factored like this: a 3 − b 3 = (a − b) (a 2 + a b + b 2 ).Notice the signs shown in red. The binomial on the right has the same sign as the binomial on the left and the trinomial on the right has the opposite sign. |
You can easily verify both these factors by multiplying out the right hand sides and noticing that all the terms except the cube terms cancel. Here are some examples. In each case we recognize the form a 3 ± b 3, (± is an abbreviation for “plus or minus”), then identify a and b, and then simply state the factored form.
Example: Factor x 3 + 27.
- Think of 27 as 3 3.
Then this is a sum of cubes and we can apply the sum of cubes formula:
a 3 + b 3 = (a + b) (a 2 − a b + b 2 ).
- Substituting a = x and b = 3 into the formula yields:
x 3 + 27 = (x + 3) (x 2 − 3 x + 9).
Example: Factor 8 x 6 − 64 y 3.
- Think of 8 x 6 as (2 x 2 ) 3
and 64 y 3 as (4 y) 3.
Then this is a difference of cubes and we can apply the difference of cubes
formula:
a 3 − b 3 = (a − b) (a 2 + a b + b 2 ).
- Substituting a = 2 x 2 and
b = 4 y into the formula yields:
8 x 6 − 64 y 3 = (2 x 2 − 4 y) (4 x 4 + 8 x 2 y + 16 y 2 ).